Que levanten la mano los que crean que “en matemáticas está todo inventado”. Venga, sin miedo que aquí estamos para aprender.
Pues no, las matemáticas son una ciencia muy viva con una gran actividad investigadora (y, por el momento, España está entre los primeros puestos en investigación matemática). Sin embargo, aún quedan muchos problemas para los que no se conoce solución, o para los que se busca una solución mejor.
Hoy contaremos un ejemplo de problema muy fácil de entender, pero aún sin resolver, el problema de las distancias enteras en el plano. Empecemos por la siguiente pregunta:
¿Cuántos puntos se pueden colocar en el plano de manera que la distancia entre cualquier par de puntos sea un número entero?
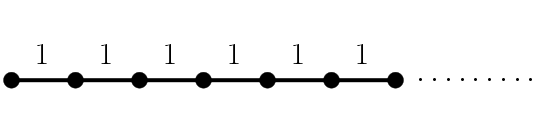
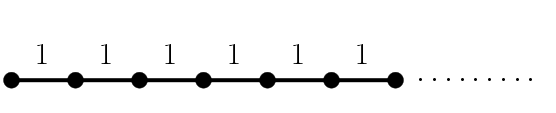
Así sin más, la respuesta es muy fácil. Piénsalo un poco… ¿La tienes? Bastaría con poner puntos alineados, por ejemplo a lo largo de una recta horizontal, cada uno a distancia 1 del siguiente. Así podríamos colocar infinitos puntos con distancias enteras entre todos ellos.
Y entonces podemos preguntarnos
¿Hay alguna otra manera, que no sea sobre una recta, de colocar infinitos puntos en el plano con distancias enteras entre todos ellos?
En 1945 Erdős (un matemático muy particular) y Anning demostraron que no, que sólo puede haber infinitos puntos con distancias enteras si éstos están alineados. Además, también demostraron que para cualquier número (finito) (n), se pueden colocar (n) puntos en el plano con distancias enteras entre ellos.
Eso sí, para ello tenían que colocar todos los puntos sobre una circunferencia. Así que después de publicar este resultado en 1945, Erdős modificó la pregunta inicial. Lo verdaderamente interesante era:
¿Cuántos puntos se pueden colocar en el plano, sin que haya tres en una misma recta ni cuatro en una misma circunferencia, de manera que la distancia entre cualquier par de puntos sea un número entero?
Vamos a intentar responder a esta pregunta. Con 2 puntos todo el mundo sabe hacerlo 🙂
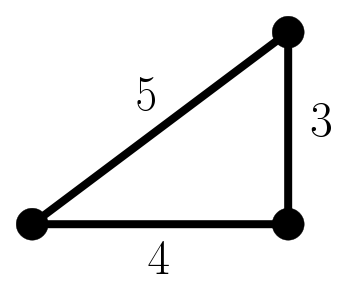
Ahora inténtalo con 3 puntos. ¿Ya lo tienes? Sirve cualquier triángulo rectángulo cuyas longitudes de los lados formen una terna pitagórica. Por ejemplo:
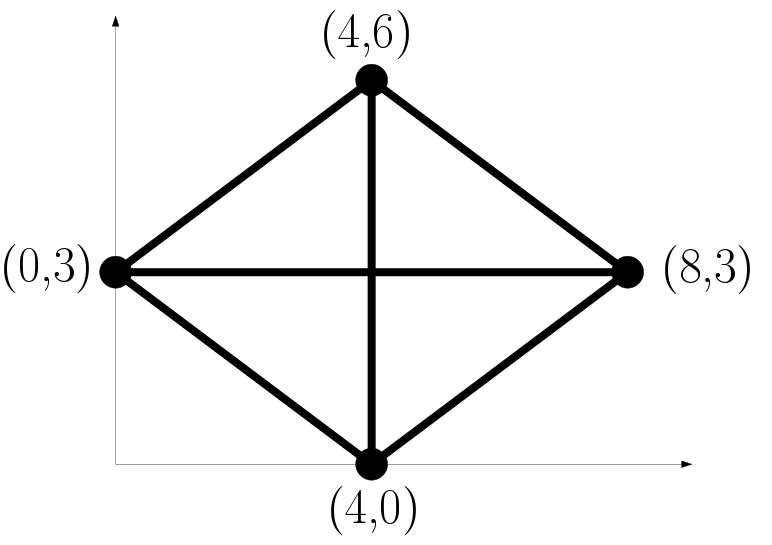
Con 4 puntos es un poco más difícil, pero no mucho. Después de un rato pensando, se nos puede ocurrir usar cuatro triángulos como el anterior para obtener:
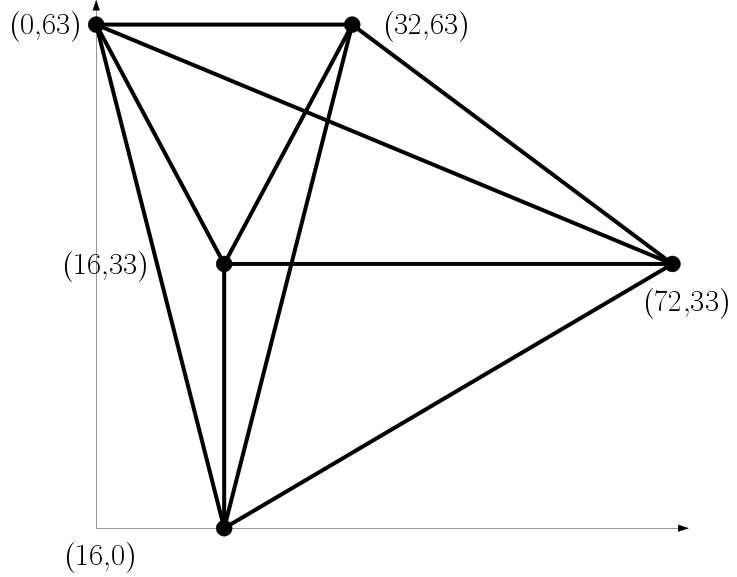
Con 5 puntos la cosa ya se complica más y no pretendemos que lo resuelvas, pero si quieres puedes comprobar que los puntos de la siguiente figura cumplen la propiedad:
Para 6 puntos también se puede hacer, si quieres comprobarlo puedes mirar este enlace.
Para 7 puntos, Kreisel y Kurz encontraron la manera de hacerlo, que puedes ver también en este otro enlace. Lo llamativo es que para ello necesitaron varias buenas ideas y unas cuantas horas de cálculo por ordenador… y su resultado es de 2007. Es decir, más de 60 años después de la pregunta original de Erdős.
¿Y para 8 puntos? Pues, aunque no te lo creas:
Nadie sabe si es posible colocar 8 puntos en el plano, sin que haya tres en una misma recta ni cuatro en una misma circunferencia, con distancias enteras entre todos ellos.
Así que aquí tienes un problema de matemáticas que es bien fácil de entender y que sigue sin resolverse, en el que siguen trabajando investigadores de todo el mundo. ¡¡Y eso que son sólo 8 inofensivos puntos!! 😉
Puedes seguirnos en Twitter, Facebook y Google +.
Nota 1: Esta entrada participa en la edición 3.14159265 del Carnaval de Matemáticas cuyo blog anfitrión es pimedios La aventura de las matemáticas.
Nota 2: Esta entrada ha llegado a portada en Menéame.

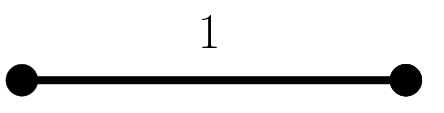

Deja una respuesta