Ayer le explicabas a tu cuñado que una integral no era más que una suma y le sugerías cómo usarla para sumar velocidades en una curva de la Fórmula 1. Hoy tu cuñado te hace ver que tenías un error, porque pueden pasar cosas raras cuando sumas velocidades y en el eje horizontal tienes una distancia. ¡¡Caminar durante 2 kilómetros a 2 km/h es más rápido que caminar un kilómetro a 1 km/h y otro a 3 km/h!! Entre los dos, intentaréis explicar lo que pasa y cómo usar entonces integrales en los datos de telemetría de la Fórmula 1.
Es lunes por la tarde. Cuando suena el teléfono y ves que es tu cuñado recuerdas que ayer, mientras veíais la Fórmula 1, le explicaste qué es una integral.
Cuñado: Oye, que le he estado dando vueltas a lo de la integral que me contaste ayer, y unos amigos en el trabajo me han dicho que hay algo que no les cuadra.
Tú: Puede ser, no te digo que no. Me centré en dar la idea de lo que es una integral y a lo mejor se me ha escapado algo.
Cuñado: Por lo que me han dicho, el problema es que en el eje horizontal teníamos una distancia (en nuestro caso la longitud de la curva) y estábamos sumando velocidades a lo largo de esa distancia.
Me han puesto un ejemplo, pero después de pensar un rato he encontrado otro que me parece más claro. Imagina una curva que mide 2 kilómetros y que tú y yo la recorremos andando (ya sabes que no tenemos dinero ni para acercarnos a un Fórmula 1).
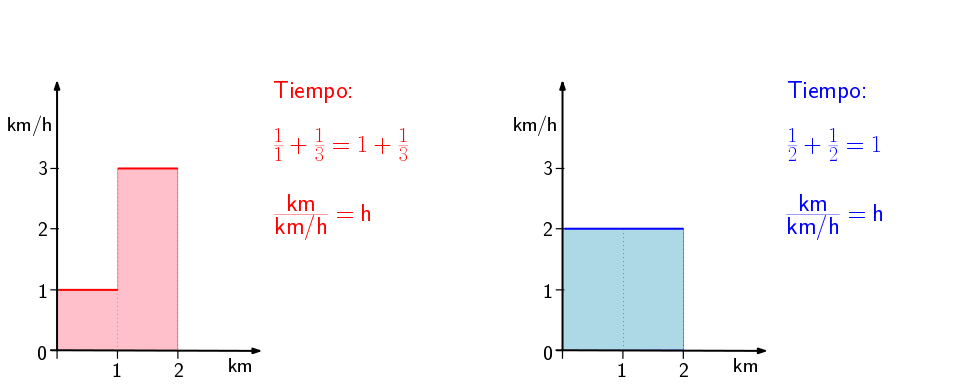
Tú, que vas de rojo, haces el primer kilómetro a una velocidad constante de 1 km/h y el segundo a una velocidad constante de 3 km/h.
Yo, que voy de azul, hago todo el recorrido a una velocidad constante de 2 km/h.
Nuestra suma de velocidades, calculada como la integral, es la misma (el área bajo nuestras dos gráficas es la misma). ¡¡Pero eso no significa que tardemos el mismo tiempo!! Verás:
Yo (azul) hago 2 kilómetros a una velocidad de 2 km/h, así que tardo exactamente una hora.
A ti (rojo) sólo el primer kilómetro ya te lleva una hora, porque vas a 1 km/h. A eso le tienes que sumar lo que tardes en el segundo kilómetro, así que está claro que vas a tardar más que yo.
O sea ¡¡caminar durante 2 kilómetros a 2 km/h es más rápido que caminar un kilómetro a 1 km/h y otro a 3 km/h!!
Tú: Pues tienes toda la razón. Comparar las sumas de velocidades a lo largo de una distancia no es buena idea.
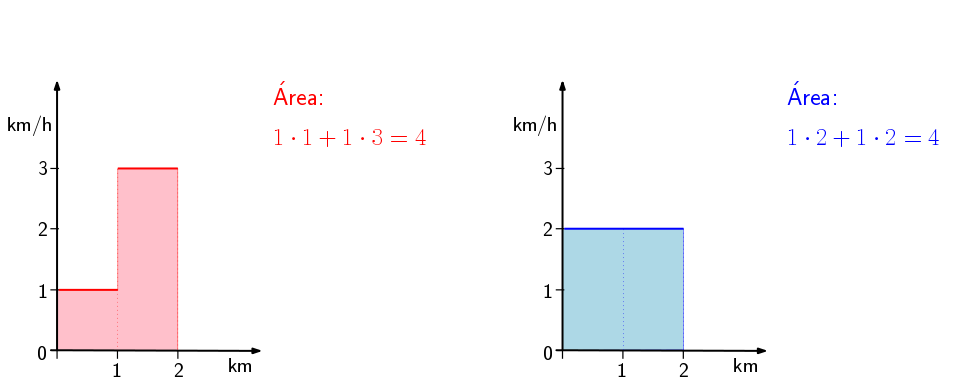
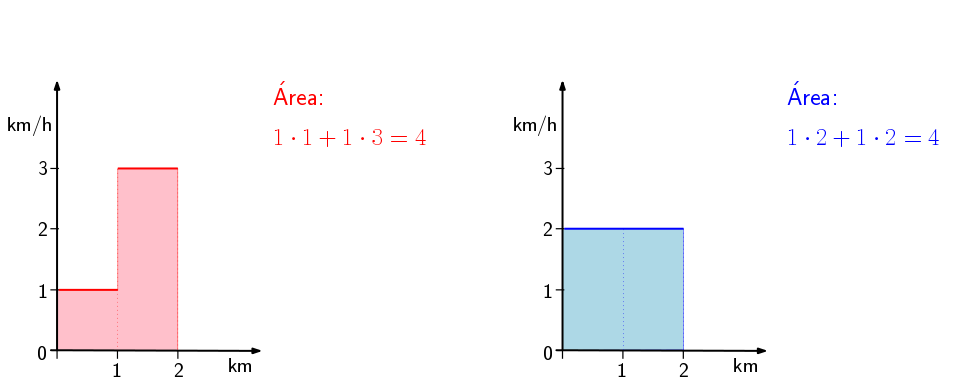
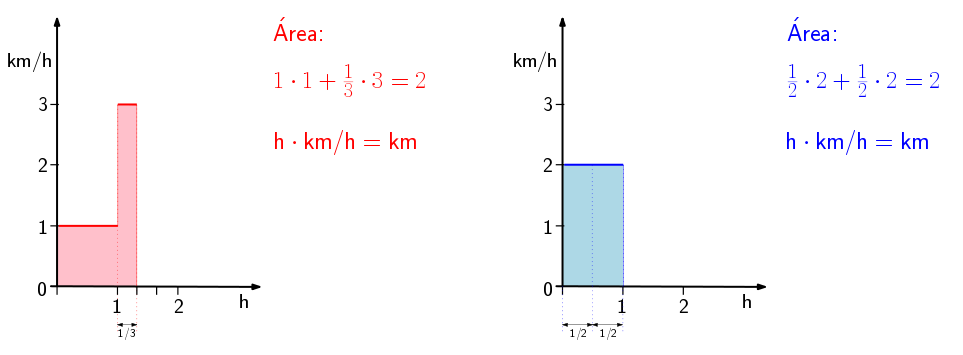
Cuñado: Mis amigos proponían poner el tiempo en el eje horizontal. O sea, comparar las sumas de velocidades a lo largo de un tiempo. En el ejemplo anterior tú vas primero a 1 km/h durante 1 hora y luego a 3 km/h durante 1/3 de hora. Yo voy a 2 km/h durante 1 hora. Quedaría así:
Como ves, esa integral da el mismo resultado (área) en los dos casos, los 2 kilómetros que hemos recorrido ambos. Pero podemos dividirlo entre el tiempo que hemos tardado, es decir, la parte del eje horizontal que hemos usado cada uno y con eso tendríamos que tu velocidad media es
[color{red}{frac{2 mbox{km}}{4/3 mbox{h}}=frac{6}{4} mbox{km/h}=1.5 mbox{km/h}}]
y la mía es
[color{blue}{frac{2 mbox{km}}{1 mbox{h}}=2 mbox{km/h}}]
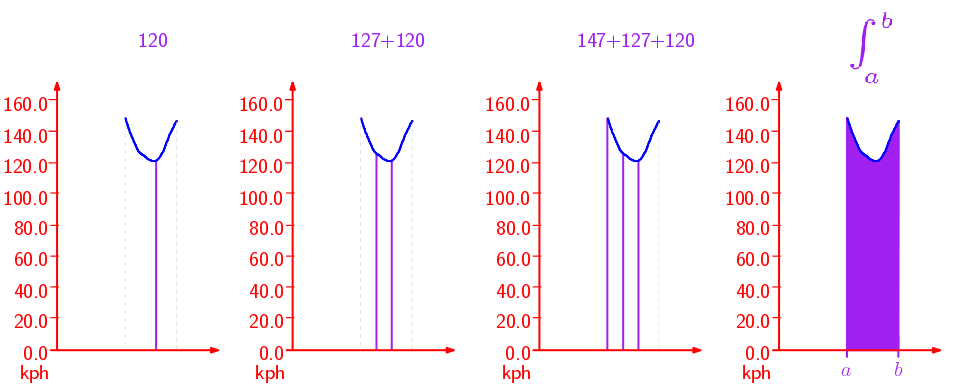
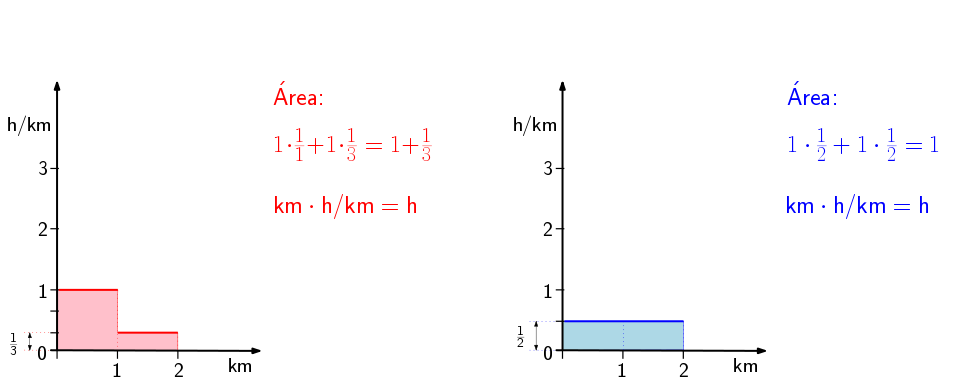
Tú: Lo malo es que en la telemetría no tenemos el tiempo en el eje horizontal, sino la distancia 🙁 Pero quizá podamos arreglarlo… Vamos a pensar cómo hacerlo en nuestro ejemplo, que es más fácil. En la primera figura calculábamos el área de cada rectángulo, multiplicando su base por su altura.
En la segunda figura calculábamos los tiempos que, si te fijas, son el resultado de dividir la base entre la altura. Esto es lo mismo que multiplicar la base por el inverso de la altura. Eso sí, para poder hacer esto necesitamos que la altura, es decir, la velocidad, no sea cero (por aquello de que no se puede dividir por cero).
De esta manera el área (o sea, la integral) será el tiempo que ha tardado cada uno. Ahora sí que esa integral refleja que tú has sido más rápido que yo.
Cuñado: ¿Y entonces esto lo podemos usar en la telemetría?
Tú: Podríamos integrar la función recíproca de la velocidad. Aunque no aparezca en la telemetría, bastaría con hacer el recíproco 1/velocidad para cada dato de velocidad. En esa nueva función cada barra vertical sería como uno de los rectángulos de la figura anterior, pero con una base infinitamente pequeña.
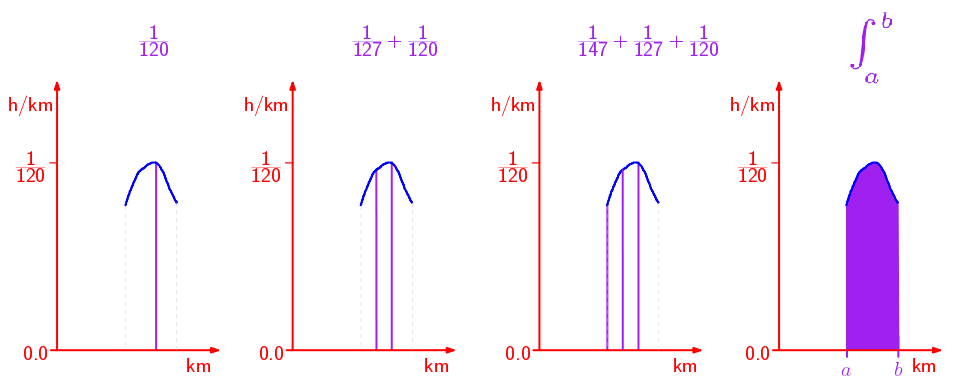
La integral entonces nos daría el tiempo que ha tardado cada piloto en recorrer la curva. Mira, aquí hay un artículo del MIT en el que utilizan esta integral para optimizar la trazada.
Cuñado: Pues tiene buena pinta, se lo voy a contar a mis amigos a ver qué dicen.
Tú: Diles que siento la equivocación y dales las gracias. Diles también que con esto sólo busco aprender y ayudar a aprender, y que de los errores también se aprende.
Cuñado: Lo haré, pero que sepas que el próximo domingo pagas tú las cañas.
Tú: Eso está hecho.
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Nota 1: Vuelvo a agradecer todos los comentarios en la entrada anterior, especialmente los de Javier y Miquel, que me hicieron ver que tomar la suma de velocidades a lo largo de la distancia no era buena idea. Me había centrado en explicar el concepto de integral y pasé por alto la interpretación física de la misma. He tratado de hacer lo mismo que cuando me equivoco en clase; reconocerlo, analizar el fallo, intentar explicarlo de la manera más clara posible y aprovecharlo para aprender. Mis alumnos suelen agradecerlo y espero que mis lectores también. Acepto que así nunca llegaré a tertuliano profesional 🙂
Nota 2: Esta entrada también participa en la edición 4.1231056 del Carnaval de Matemáticas, cuyo anfitrión es el blog Scientia.
Para saber más:
Al hacer la integral a lo largo de una distancia (en la primera y la segunda figura) todos los palitos verticales que estamos sumando tienen el mismo tamaño de la base, un infinitésimo de distancia.
Al hacer la integral a lo largo de un tiempo (en la cuarta figura) todos los palitos verticales también tienen el mismo tamaño de la base, en este caso un infinitésimo de tiempo.
En ambos casos estamos sumando km/h, pero en el primer caso todos los sumandos tienen en común el numerador de esos km/h (infinitésimo de distancia), mientras que en el segundo caso lo que tienen en común es el denominador de esos km/h (infinitésimo de tiempo). Y como en los km/h la unidad está en el denominador (son los kilómetros recorridos en una hora), lo que necesitamos que sea común es el denominador.
Por eso la integral no da problemas cuando en el eje horizontal tenemos lo mismo que en el denominador del eje vertical, como en la tercera figura (h frente a km/h) o como en las dos últimas figuras (km frente a h/km).
En otro comentario que ha llegado cuando ya tenía casi terminada esta entrada , Miquel propone una solución para tener el tiempo en el eje horizontal: Pasar de una función tipo «velocidad en función de la posición (v(x))» (como la de las gráficas de telemetría) a la función «posición en función del tiempo (x(t))». Luego para obtener la función «velocidad en función del tiempo (v(t))» sólo tendrías que derivar x(t).


Deja una respuesta