Es probable que hayas visto una imagen que anda por ahí diciendo que los decimales de Pi contienen cualquier información que haya existido o pueda existir. Quizá te preguntes si es cierto y la verdad es que para el número Pi no se puede asegurar, porque está relacionado con un problema matemático aún sin resolver. Pero sí hay otros números para los que el meme sería cierto… aunque resulten menos glamourosos que Pi.
Desde hace algún tiempo circula por internet un meme que dice algo así como que toda la información que haya existido o pueda existir en un futuro está contenida en los infinitos decimales de Pi.
Bonito, ¿verdad? Si sigues leyendo, primero encontrarás una explicación de lo que dice el meme, después verás que hay un par de fallos en su razonamiento y, por último, descubrirás cómo arreglarlos fácilmente para hacer que el meme sea cierto. ¿Te apuntas?
Primero la explicación del meme:
Lo que dice el meme es que el número Pi
- Tiene infinitos decimales
- y esos decimales no son periódicos, o sea, que no hay un bloque de cifras que se repita indefinidamente.
Y por eso cualquier combinación de números imaginable tendrá que aparecer, en algún momento, en esa ristra de decimales.
Como cualquier información se puede traducir a números (por ejemplo usando ASCII o mapas de bits)… ¡Voilà! esa ristra de decimales contendrá:
El nombre de todas las personas a las que vayas a amar, la fecha, hora y manera de tu muerte y las respuestas a todas las grandes preguntas del universo. Lo primero que viste en este mundo, lo último que verás antes de que tu vida te abandone, y todos los momentos, trascendentales y mundanos, que vayan a ocurrir entre esos dos puntos. Toda la información que haya existido o vaya a existir, el ADN de cualquier ser en el universo.
Ahora un primer fallo en el razonamiento del meme:
Fíjate en este número 
que, como ves, está formado por grupos de ceros con un uno al final (y cada grupo tiene un cero más que el anterior).
Este número también
- Tiene infinitos decimales y
- esos decimales no son periódicos (porque ningún bloque de números se repite indefinidamente).
Pero ya te habrás dado cuenta de que ¡¡el número 2 jamás aparecerá en esa ristra de decimales!! Así que tener infinitos decimales no periódicos, como dice el meme, no garantiza contener cualquier información.
Después un segundo fallo en el razonamiento del meme:
Ahora ya estás convencido de que tu ristra de decimales tiene que contener todos los números 0,1,2,…,9. Si los buscas en los decimales de Pi, pronto encontrarás todos esos números…
… pero resulta que con eso tampoco basta.
Imagina que en tu ristra de decimales hubiera muy pocos nueves:
- A lo mejor resulta que el sentido de la vida se escribe con muchos nueves. Y entonces no podría estar escrito entre tus decimales.
- Así que tu ristra de números no puede tener pocos nueves. De la misma manera, tampoco puede tener pocos ochos, ni pocos sietes…
Total, que ningún dígito del 0 al 9 puede aparecer menos veces que los demás.
Ahora imagina que en tu ristra de decimales hubiera muy pocos dieciochos.
- A lo mejor resulta que la película de tu vida se escribe con muchos dieciochos. Y entonces no podría estar escrita entre tus decimales.
- Así que tu ristra de números no puede tener pocos dieciochos. De la misma manera, tampoco puede tener pocos veintiunos, ni pocos treinta y cincos…
Total, que ningún grupo de dos dígitos del 00 al 99 puede aparecer menos veces que los demás.
Y ya te imaginas que lo mismo pasa para grupos de tres dígitos, grupos de cuatro dígitos, etcétera…
Esta propiedad, que como ves hace falta para que el meme sea correcto, se llama ser normal. ¡¡Y no se sabe si Pi es o no un número normal!!
De hecho, éste es uno de tantos problemas sin resolver en matemáticas. No resulta fácil demostrarlo, porque comprobar algo para esos infinitos decimales es un poco… digamos… complicado (salvo que seas Chuck Norris). Pero todos los indicios apuntan a que Pi sí es normal.
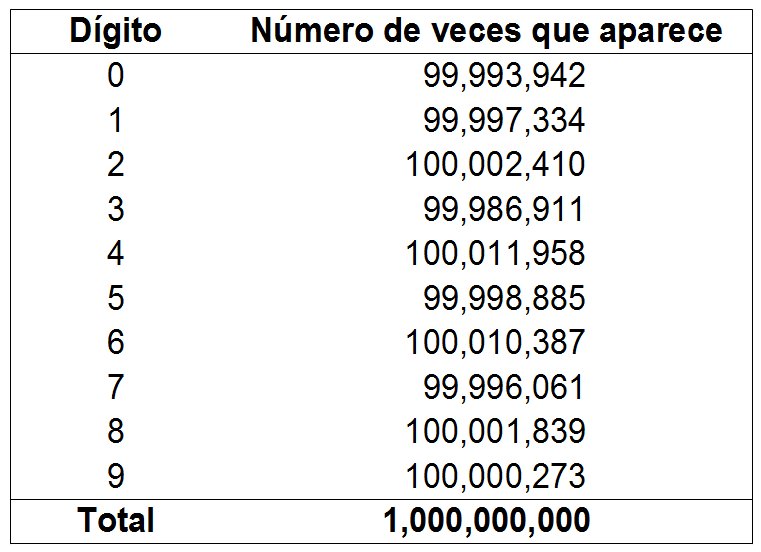
Por ejemplo, se ha comprobado cuántas veces aparece cada dígito del 0 al 9 en el primer millardo de dígitos de Pi. Y todos aparecen un número de veces bastante parecido (aunque esto no demuestra nada, es sólo un indicio).
Y por último cómo arreglar fácilmente esos fallos y hacer que el meme sea cierto:
Por suerte, hay otros números para que sí se ha podido demostrar que son normales. Después de lo anterior, te puede parecer que tienen que ser una cosa complicadísima, pero aunque parezca mentira puedes conseguir un número normal de una forma muy sencilla.
Sólo tienes que usar como decimales la concatenación de todos los números naturales 
Este número se conoce como constante de Champernowne, por el matemático y economista inglés David Gawen Champernowne, que fue quien demostró (en 1933) que este número era normal.
Pero, claro, Pi queda más místico y un meme con el número de Champernowne probablemente no se habría convertido en un meme… ¿Alguien se anima a intentarlo?
Recuerda que puedes seguirnos
en Twitter, en Facebook y en Google +
Nota 1: Esta entrada ha llegado a portada en Menéame. ¡Gracias!
Nota 2: Esta entrada ha llegado a portada en Divúlgame. ¡Gracias!
Nota 3: Esta entrada quiere contribuir al día de Darwin, en el 205 aniversario de su nacimiento, que se celebra con la intención de promover la ciencia.
Para saber más:
Pi no es el único número del que no se sabe si es normal o no. Sucede lo mismo para muchos otros números (irracionales), como (e) o (sqrt{2}). Es más, ni siquiera se sabe si en los decimales de (sqrt{2}) el dígito 1 aparece infinitas veces o no. Quizá te interese el artículo Old and new results on normality, de Martine Quefféec. Si lo tuyo es el número Pi, puedes buscar el libro Pi: A source book.
Pero también hay más números que sí se sabe que son normales, como el número de Copeland-Erdős, que se obtiene concatenando los números primos 
A lo mejor éste tendría más éxito como meme, por aquello de usar los números primos. Si quieres, puedes echar un vistazo al artículo en el que Copeland y Erdős introdujeron este número. Quizá también te interese el artículo original de Champernowne. También Alan Turing trabajó sobre este tema; aunque su manuscrito no llegó a publicarse, algunos autores lo han completado y publicado en el artículo Turing’s unpublished algorithm for normal numbers.
Y la cosa puede complicarse todavía un poco más. Cuando se dice que un número es normal, quiere decir que lo es respecto de la base numérica en que esté escrito (en todo lo anterior se habla sólo de la base 10, la más común). Pues resulta que hay números que sí son normales en una base pero en otra no lo son, como los números de Stoneham. Puedes comprobarlo en el artículo Nonnormality of Stoneham constants, de David H. Bailey y Jonathan M. Borweiny.
Para liarlo un poco más, casi todos los números reales son normales (los que no lo son forman un conjunto de medida de Lebesgue cero). En ese sentido, ser un número normal es «lo normal». Lo demostró Émile Borel en 1909, en su artículo Les probabilités dénombrables et leurs applications arithmétiques.
Si tuvieras un dado de diez caras, numeradas del 0 al 9, y fueras Chuck Norris, podrías tirar el dado infinitas veces e ir apuntando los números que te salieran. Estarías generando una ristra aleatoria de infinitos decimales, en la que podrías comprobar que todos los números del 0 al 9 habrían salido el mismo número de veces (niños, no intentéis esto en casa). Lo mismo pasaría con los bloques 00 al 99, etcétera. Es decir, obtendrías un número normal. Por eso los números normales tienen cierto «regusto» aleatorio, aunque son dos cosas diferentes; ya ves que el número de Champernowne tiene muy poco de aleatorio.
Por último, como sobre este tema se ha publicado mucho (y muy bueno), aquí van algunas entradas de las que aprender un poco más.
Sobre la idea de fondo en el meme, puedes leer Todos los números están en pi, en Microsiervos, y/o Mensajes ocultos en pi, de Tio Petros, y/o Mensajes ocultos en el universo a revelar por las matemáticas, de Alfonso de la Fuente, y/o Cuántas cosas en tan poco espacio, en Naukas, donde también puedes encontrar la advertencia ¡Precaución!: NO calcular Pi en binario.
Sobre números normales puedes leer Número normal, en Gaussianos, y/o No se sabe si todos los números naturales están en Pi (o sobre los números anormales), en La Ciencia de la Mula Francis.
También puede interesarte leer El algoritmo de Chudnovsky, o cómo se calculan los decimales de Pi en el siglo XXI, en Gaussianos, para entender mejor que este número no es aleatorio.
Ya en inglés, puedes leer Your Life in Pi, en Slate, donde se sitúa el origen del meme en Reddit. También pueden interesarte los vídeos Are Shakespeare’s Plays Encoded within Pi? y Two Non-Repeating Non-Normal Numbers, de Vi Hart en YouTube.
También puede interesarte saber que el asunto del meme ha llegado hasta The Huffington Post, en cuya sección de ciencia han escrito sobre ello: Pi Meme Misleading About Mathematical Constant, Experts Say.
Vuestras aportaciones:
En los comentarios, afterBeatles envía el enlace a una aplicación web que permite codificar los decimales de Pi para obtener resultados textuales, visuales o sonoros. En Google +, Nancho Álvarez envía el enlace a un pifs, un sistema de archivos que guarda tus datos en Pi.
Imágenes:
La imagen del meme de Pi está tomada de reddit, donde el autor da su permiso para utilizarla libremente. La imagen de decimales de Pi está tomada de fdecomite, en Flickr. La imagen de los dígitos del 0 al 9 está tomada de Denise Krebs, en Flickr. La imagen de los grupos de dos dígitos del 00 al 99 está tomada de Tom Magliery, en Flickr.
Deja una respuesta