Volvamos por un momento a aquella tierna infancia en que todo era nuevo y rebosabas ganas de aprender. Trata de recordar ese día en que te enseñaron a distinguir las figuras geométricas: Esto es un círculo, aquello un triángulo, lo de más allá un cuadrado. Si, unos años más tarde, al niño que llevas dentro todavía le quedan ganas de aprender, con esta entrada descubrirás una nueva figura que nunca te enseñaron, el pseudo-triángulo.
Si los niños aprenden jugando, ¿por qué no vamos a hacerlo los mayores? Ya en la anterior entrada (que te recomiendo leer para disfrutar más de ésta) te propuse un juego en el que, uniendo puntos y como quien no quiere la cosa, acababas dibujando triángulos y aprendiendo lo que es una triangulación. Ahora te propongo un juego parecido para descubrir qué es un pseudo-triángulo.
Para empezar, tienes que dibujar unos cuantos puntos en tu papel o en tu pantalla. Yo voy a usar los de la entrada anterior, pero tú puedes dibujar los que quieras.
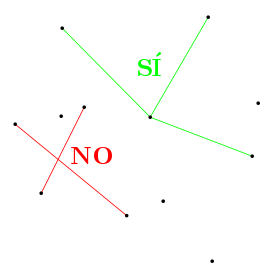
Lo siguiente será dibujar uniones en línea recta (segmentos) entre esos puntos, pero con un par de condiciones. La primera es que, como en la entrada anterior, no puede haber cruces. Allí te proponía que pensaras que las uniones son cables y no se te pueden cruzar:
¿Fácil, verdad? La segunda condición también es muy sencilla. En cada punto tiene que haber un ángulo de 180 grados sin ninguno de esos cables:
Vamos, que los segmentos que salen de un punto tienen que ser algo así como las varillas de un abanico:
Como los matemáticos somos así de originales, cuando un punto cumple esta segunda condición decimos que es puntiagudo.
Y ahora ya puedes ponerte a dibujar. Empieza con un segmento, luego otro, y otro más… ¡¡pero cumpliendo esas dos condiciones!! La regla de este juego es la siguiente:
Une en línea recta los puntos, dibujando tantos segmentos como puedas, sin que haya ningún cruce y de manera que todos los puntos sean puntiagudos.
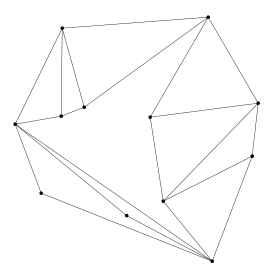
Como siempre, te animo a que hagas tu propio dibujo con todos los segmentos que puedas. Cuando ya no puedas añadir ningún segmento más (respetando esas condiciones) tendrás un grafo plano puntiagudo maximal.
¿Quieres saber si lo has hecho bien? Pues estás de suerte, porque hay una forma muy fácil de comprobarlo. Comprueba que no hay cruces, que todos los puntos son puntiagudos y que tienes este número de segmentos:
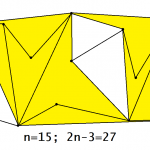
Si (color{red}{n}) es el número total de puntos, en un grafo plano puntiagudo maximal hay (2cdotcolor{red}{n}-3) segmentos.
En mi ejemplo había (color{red}{n=12}) puntos, así que debería haber (2cdotcolor{red}{12}-3=21) segmentos. Si quieres, puedes contarlos y comprobar que no hay cruces y que en todos los puntos hay un ángulo de más de 180 grados:
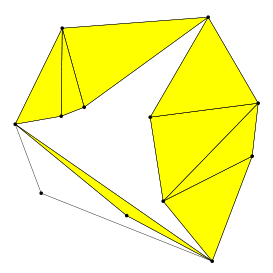
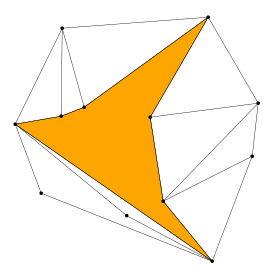
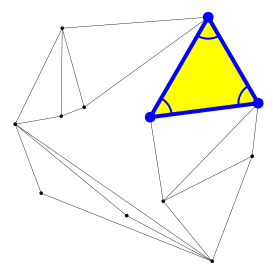
Ahora mira las figuras geométricas que han aparecido en tu dibujo. Tendrás algunos triángulos:
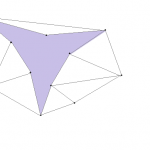
Y es muy probable que también tengas alguna otra figura, parecida a ésta:
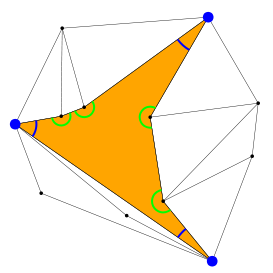
¿Adivinas qué figura es? ¡Bingo! Es un pseudo-triángulo y para reconocerlo sólo tienes que saber esto:
En el interior de un pseudo-triángulo hay exactamente tres ángulos de menos de 180 grados.
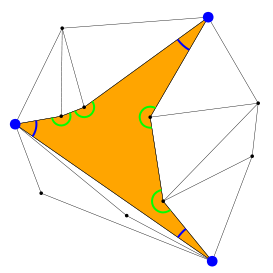
Voy a enseñarte algunos ejemplos. Para empezar, podemos comprobar que la figura de antes es de verdad un pseudo-triángulo:
Como ves, tiene exactamente tres ángulos de menos de 180 grados (marcados en azul) y todos los demás ángulos son de más de 180 grados (marcados en verde). A los vértices «azules», con ángulos de menos de 180 grados, se les llama esquinas del pseudo-triángulo. La definición de pseudo-triángulo nos dice que:
Un pseudo-triángulo tiene exactamente tres esquinas.
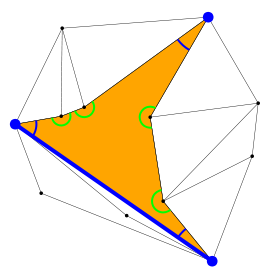
Ahora fíjate en una cosa; esas esquinas pueden estar unidas directamente, por un solo segmento:
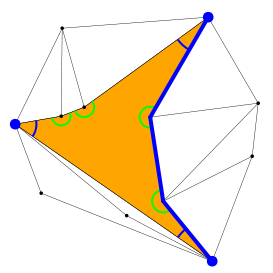
o pueden estar unidas por una cadena de segmentos «combada hacia adentro» (técnicamente «convexa hacia adentro»):
Estas dos posibilidades se pueden combinar de cualquier manera. En el ejemplo anterior aparecían los dos tipos de uniones, pero también puede que sólo aparezca una de ellas. Por ejemplo, que todas las esquinas estén unidas por cadenas convexas hacia adentro, como en la figura que aparece en la entrada de la Wikipedia
o que todas las esquinas estén unidas directamente, por un solo segmento
y entonces lo que tienes es ¡¡un triángulo!! Porque los triángulos tienen exactamente tres ángulos de menos de 180 grados y, por eso:
Un triángulo es un tipo particular de pseudo-triángulo.
¿A que ya tienes claro lo que es un pseudo-triángulo? Pues entonces vas a entender enseguida lo que es una pseudo-triangulación. No es más que un dibujo como el tuyo, en el que un conjunto de puntos queda rellenado por pseudo-triángulos (igual que cuando se rellenan con triángulos se llama triangulación).
De hecho, lo que has dibujado es una pseudo-triangulación puntiaguda, porque todos los puntos son puntiagudos:
Todo grafo plano puntiagudo maximal es una pseudo-triangulación puntiaguda. Si (color{red}{n}) es el número total de puntos, tiene (2cdotcolor{red}{n}-3) segmentos y (color{red}{n}-2) pseudo-triángulos.
Así que hoy no te acostarás sin saber una cosa más… y, mejor aún, podrás decir que de esto sabes más que Wolfram Alpha :-).
Puedes seguirnos en Twitter, Facebook y Google+.
Nota 1: Ya sé que tienes poco tiempo (a mí me pasa lo mismo), pero me haría mucha ilusión que recompensaras esta entrada enviando tu dibujo al correo cifrasyteclas@km77.com, por Twitter, por Facebook o por Google+. Iré añadiendo vuestras pseudo-triangulaciones en una galería al final. ¡Gracias!
Nota 2: Esta entrada participa en la edición 4.1231 del Carnaval de Matemáticas, cuyo blog anfitrión es Matemáticas interactivas y manipulativas.
Nota 3: Esta entrada no ha llegado a ningún agregador, pero ha llegado aún más lejos; a los alumnos de 1º de Bachillerato del IES Profesor Tierno Galván de Alcalá de Guadaíra (Sevilla). La ha llevado hasta ellos Joaquín García Mollá (@imatematicas en Twitter), uno de esos profesores que todo el mundo querría haber tenido (como puedes comprobar en su blog). Desde aquí, mi agradecimiento a esos chicos por sus ganas de aprender y a Joaquín por sus ganas de enseñar.
Imagen del abanico: Wikimedia Commons.
Para saber más:
Quizá te hayas fijado en que, cuando miramos los ángulos de un pseudo-triángulo, no hablamos de ángulos iguales a 180 grados. Esto es porque se suele considerar que en el conjunto de puntos no hay tres puntos alineados (sobre una misma recta). Se dice entonces que el conjunto está en posición general.
Si en tu dibujo sólo han aparecido triángulos y no hay ningún pseudo-triángulo, es porque has dibujado los puntos de una manera muy particular. La única manera de que pase eso es tener puntos en posición convexa, es decir, que su envolvente convexa (de la que hablábamos en la entrada anterior) no tenga ningún punto dentro.
Las pseudo-triangulaciones cumplen muchas de las propiedades de las triangulaciones, con la ventaja de tener menos aristas, y tienen aplicaciones en detección de colisiones entre objetos en movimiento, en rigidez o en vigilancia de regiones con el menor número posible de guardias.
Esta estructura ha suscitado mucho interés entre los investigadores en los últimos años y, en particular, son uno de mis temas favoritos, al que dediqué la mayor parte de mi tesis doctoral (el primer capítulo, también en español, puede ser una buena iniciación). Para saberlo casi todo sobre pseudo-triangulaciones, la referencia es este artículo de Rote, Santos y Streinu. Si te interesan, no dudes en preguntarme.










Deja una respuesta