Seguro que has hecho alguna vez un dibujo del tipo «une los puntos». Te dan un conjunto de puntos y una condición, unir cada punto con el siguiente, para descubrir el dibujo escondido. Esta entrada te propone un juego parecido con el que podrás divertirte y, a la vez, aprender matemáticas. Sólo tienes que buscar lápiz y papel (es un decir), dibujar unos puntos y unirlos con una condición. ¿Te animas?
En el juego de «une los puntos» no puedes elegir dónde dibujar los puntos, porque te los dan ya dibujados. Además cada punto te lo dan con un número, algo así:
La regla del juego es muy sencilla:
Une en línea recta cada punto con el siguiente, de acuerdo con los números.
Cuando terminas tienes un dibujo, más o menos interesante. Entre nosotros, ¿cuánto hace que no juegas a esto? ¿Quieres intentarlo? 🙂 Si no tienes tiempo o te puede la impaciencia, también puedes pinchar aquí para ver la solución.
En el juego matemático que te propone esta entrada vas a tener más libertad, porque el conjunto de puntos lo vas a dibujar tú. Anímate, toma lápiz y papel, y ponte a dibujar puntos. Los que quieras. Como quieras. ¿Qué mas quieres? Eso sí, ten en cuenta que cuantos más puntos dibujes, más uniones tendrás que hacer.
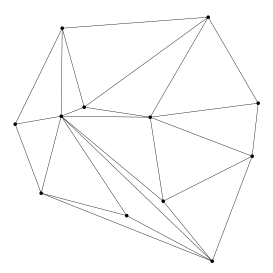
¿Ya los has dibujado? Pues ya tienes tu tablero de juego, porque aquí no vamos a necesitar poner un número a cada punto. Eso que te ahorras. Mi tablero de juego tiene 12 puntos y esta pinta:
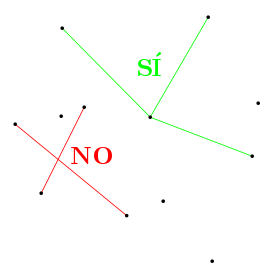
Una vez que tienes tu tablero, lo siguiente es saber cuáles son las reglas de este juego. Vas a tener que unir los puntos en línea recta, como antes, pero con una condición; que no haya cruces. Los cruces ya aparecieron en este blog, pero si te lo perdiste o no te acuerdas, no te preocupes. Piensa que estás uniendo los puntos con cables y tienes que evitar que se te crucen. Sí puede haber varios cables conectados a un mismo punto, pero los cables no se pueden cruzar.
¿Está claro? Pues venga, a dibujar. Empiezas con un segmento, luego dibujas otro, después haces otro más… El juego va a consistir en dibujar todos los que puedas. Cuantos más, mejor, ¡¡pero sin que se te crucen los cables!! La regla de este juego sería:
Une en línea recta los puntos, dibujando tantos segmentos como puedas sin que haya ningún cruce.
Déjame animarte otra vez a que lo hagas tú mismo, que es mucho más divertido.
Si lo has hecho bien, lo que acabas de dibujar sobre tu conjunto de puntos es un grafo plano maximal; «plano» porque no tiene cruces y «maximal» porque no se le puede añadir ningún segmento si quieres que siga sin haber cruces.
Si has dibujado tu propio grafo plano maximal, ver el mío no te dirá gran cosa, pero puedes verlo en este enlace. Yo he dibujado 12 puntos, pero puede que tú hayas elegido otro número. Y aunque también tuvieras 12, puede que los hayas colocado de manera distinta. Y aún hay más; aunque hubieras usado el mismo conjunto de puntos que yo, puede que tú hayas dibujado otros segmentos distintos.
Entonces, ¿cómo puedes saber si lo has hecho bien o no? Lo primero, tienes que asegurarte de que no has dibujado ningún cruce. ¿Estás seguro? Entonces tu grafo es plano.
Lo segundo, tienes que asegurarte de que no puedes dibujar ningún segmento más si quieres que siga sin haber cruces. O sea, asegurarte de que tu grafo es maximal. Mira bien tu dibujo, ¿seguro que no se puede añadir ningún segmento? A lo mejor se te está escapando alguno. ¿Estás seguro que no puede llegar un listo que todo lo sabe y dibujar otro segmento más?
Para que no te quedes con la duda, las matemáticas vienen al rescate. Sólo van a hacer falta dos números y una cuenta. El primer número es simplemente el número de puntos has dibujado, y le vamos a llamar (color{red}{n}). En mi ejemplo hay 12 puntos, así que yo tengo (color{red}{n=12}).
El segundo número tiene más gracia. Imagina que tomas una goma elástica muy pequeña y la estiiiiiiiiiiiiiras hasta que caben dentro todos los puntos que has dibujado. Ahora la pones alrededor de tus puntos y la sueltas, ¿qué pasa? Como puedes ver en esta figura animada, la goma se encogerá y se quedará anclada a algunos de los puntos.
El segundo de nuestros números será el número de puntos a los que se queda anclada la goma, y le vamos a llamar (color{green}{k}). Como ves, en mi ejemplo la goma se queda anclada en 7 puntos, así que yo tengo (color{green}{k=7}).
Para poder llamarla por su nombre después, déjame que te cuente que la figura que forma esa goma elástica cuando se queda anclada a algunos de tus puntos se llama envolvente convexa de tu conjunto (lo de «envolvente» parece claro porque la goma envuelve al conjunto, lo de «convexa» ya lo ha explicado Mati).
Y, como te prometí antes, sabiendo esos dos números y haciendo una cuenta puedes saber si tu solución es correcta o no (recuerda que ya habías comprobado que no tenía cruces):
Si (color{red}{n}) es el número total de puntos y (color{green}{k}) es el número de vértices de la envolvente convexa, en un grafo plano maximal hay (3cdotcolor{red}{n}-3-color{green}{k}) segmentos.
En mi ejemplo (color{red}{n=12}) y (color{green}{k=7}), así que debería haber (3cdotcolor{red}{12}-3-color{green}{7}=26) segmentos. Si vuelves a mirar mi solución, podrás comprobar que salen las cuentas. ¿Y en la tuya?
Podríamos terminar aquí, pero estaríamos pasando por alto un detalle muy interesante. Mira fijamente tu solución. Ahora mira fijamente la mía. Compáralas. ¿Se parecen en algo? Seguro que ya te has dado cuenta; en las dos la envolvente convexa está rellenada con triángulos. Ésta es otra propiedad de los grafos planos maximales:
Todo grafo plano maximal es una triangulación. Si (color{red}{n}) es el número total de puntos y (color{green}{k}) es el número de vértices de la envolvente convexa, en un grafo plano maximal hay (2cdotcolor{red}{n}-2-color{green}{k}) triángulos.
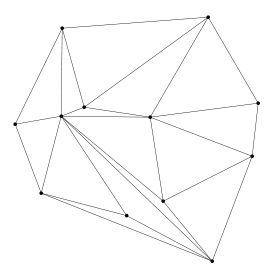
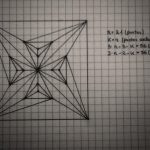
Según esto, en mi ejemplo debería haber (2cdotcolor{red}{12}-2-color{green}{7}=15) triángulos. Si a estas alturas no te he convencido de hacer tu propio dibujo, me temo que ya no voy a conseguirlo, así que creo que ya puedo enseñarte el mío:
Ahora sólo te falta comprobar que hay 15 triángulos para ver que en mi triangulación salen las cuentas.
¿Y en la tuya?
Puedes seguirnos en Twitter, Facebook y Google +.
Nota: Como en la anterior entrada sobre puntos y segmentos, nos haría mucha ilusión que nos enviaras tu dibujo a cifrasyteclas@km77.com. Iremos actualizando esta entrada para incluir todos los que nos lleguen en la galería al final de la entrada. ¡Gracias!
Para saber más:
Al preparar esta entrada me he encontrado con una original propuesta para enseñar matemáticas usando juegos del tipo «une los puntos». La idea es que para encontrar el número asociado a cada punto haya que hacer alguna operación (de ese modo, sólo puedes saber en qué orden unirlos si has resuelto bien las operaciones). Si estás buscando ideas para que tus niños aprendan matemáticas, puedes probar con ésta.
La envolvente convexa se puede definir como el conjunto convexo más pequeño que contiene a tus puntos. También se puede definir como la intersección de todos los conjuntos convexos que contienen a tus puntos. Para calcular de manera eficiente la envolvente convexa de un conjunto de puntos hay múltiples algoritmos, pues es uno de los problemas fundamentales en Geometría Computacional.
Si lo piensas un poco, que en un grafo plano maximal te quede la envolvente convexa rellenada por triángulos tiene bastante sentido. Por el exterior de la envolvente convexa no se puede dibujar ningún segmento más. Y si en el interior de la envolvente convexa alguna región no fuera un triángulo, sería un polígono y podríamos dividirlo en dos añadiendo algún segmento. Si quieres una demostración de que todo polígono se puede triangular, puedes echar un vistazo a esta página (a partir de la Figura 3).
Las triangulaciones son una de las estructuras matemáticas con más aplicaciones. Si piensas en alguna, seguro que enseguida te viene a la cabeza la geodesia o los gráficos por ordenador. Además de eso, también se usan en ingeniería en el método de los elementos finitos. Si te interesa, puedes leer más sobre la generación de mallas para este método.
Para un mismo conjunto de puntos puede haber muchas triangulaciones distintas, dependiendo de qué segmentos se escojan. De todas las triangulaciones posibles, la más destacada es la Triangulación de Delaunay. Está estrechamente relacionada con el Diagrama de Voronoi (más información en I, II y III), así que comprenderás que merezca al menos una entrada para ella sola ;-). Si no puedes esperar y quieres saber más sobre triangulaciones de Delaunay, te recomiendo este capítulo del muy recomendable libro Computational Geometry: Algorithms and Applications. En él puedes encontrar (página 193, Teorema 9.1) una demostración de los resultados que te he dado antes sobre cuántos segmentos y cuántos triángulos hay en una triangulación. También te recomiendo este artículo sobre Envolvente convexa, triangulación de Delaunay y diagrama de Voronoi de Manuel Abellanas en el ciclo de conferencias Un paseo por la Geometría.
Para terminar, es bueno resaltar que en esta entrada estamos hablando de grafos geométricos en los que los vértices se representan por puntos y las aristas se representan por segmentos en línea recta. Si permitimos representar las aristas por curvas, los grafos planos maximales seguirán teniendo regiones triangulares, pero ahora podría haber más aristas que antes (porque podría haber aristas por fuera de lo que antes era la envolvente convexa).
Vuestros dibujos:






Deja una respuesta