Seguro que en estos días has comido alguna vez roscón de reyes, incluso es posible que te hayas animado a hacerlo en casa. La tradición es que el roscón incluya una o varias figuras (el número suele depender del tamaño) y un haba, con consecuencias diversas para quien los encuentre.
Anoche me tocó empezar un roscón. Aunque siempre hay quien busca pistas para decidir por dónde cortar, en mi caso corté por un lugar al azar… y me encontré con una de las sorpresas. Esto me llamó la atención y mi curiosidad matemática saltó como un resorte. ¿Cuál es la probabilidad de encontrar una sorpresa (incluyendo el haba) al hacer el primer corte del roscón?
Por supuesto, esa probabilidad dependerá de varios factores; la forma y el tamaño del roscón, el número de sorpresas, la disposición de éstas… Vamos a centrarnos en el caso de mi roscón que, al fin y al cabo, es con el que hice el experimento 🙂
La forma de mi roscón se aproximaba bastante a una corona circular. No tengo una foto, porque cuando se me ocurrió hacerlas era demasiado tarde, pero era algo parecido a esto:
Las sorpresas estaban colocadas aproximadamente en el medio de la masa, a lo largo de una circunferencia intermedia entre la circunferencia del agujero y la circunferencia exterior del roscón. Sí tengo una foto de la bandeja, ya vacía, para estimar el radio de esa circunferencia:
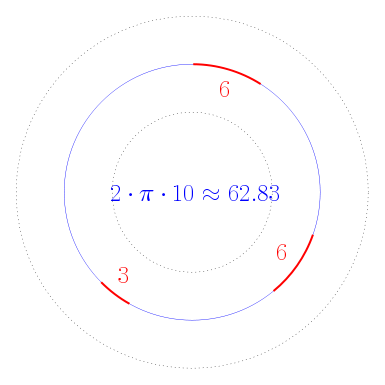
Pongamos que las sorpresas estaban a lo largo de una circunferencia de 10 centímetros de radio. Vamos a calcular la longitud de esa circunferencia; ya sabes (y si no aprovechas para recordarlo :-)) que esta longitud es (2cdot picdot 10) al ser de radio 10.
Ahora vamos a medir el tamaño de las sorpresas. Empezamos por las figuras:

Mi roscón tenía dos figuras, ambas de tamaño similar. Cada una venía envuelta en un plástico, como si fuera un caramelo, así que podemos estimar unos 6 centímetros de largo para cada figura. Además, en mi roscón no podía faltar un haba:
Ésta también venía envuelta como un caramelo, así que pongamos que su envoltorio medía unos 3 centímetros.
En total tenemos (6+6+3) centímetros para las sorpresas y (2cdot picdot 10) centímetros para el radio de la circunferencia en la que estaban colocadas. Por supuesto, todo esto es una aproximación; ni el roscón era circular, ni las medidas son exactas, ni las sorpresas se ajustaban perfectamente a la forma de una circunferencia… Pero nos sirve para hacernos una idea.
Si aceptas estas aproximaciones, vamos a estimar la probabilidad de encontrarnos una sorpresa en el primer corte. Ésta vendrá dada por el cociente entre la longitud total de las sorpresas (casos favorables) y la longitud total de la circunferencia (casos posibles).
Así que la probabilidad de encontrar una sorpresa en el primer corte de mi roscón era, aproximadamente:
[frac{6+6+3}{2cdot picdot 10}approx 0.24]
es decir, ¡¡tenía más o menos un 25% de probabilidades de encontrar una sorpresa al primer corte!! Bastante más de lo que podría pensarse en un principio 🙂 Como ves, las matemáticas están en todas partes; sólo hay que buscarlas.
Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.
Nota 1: Esta entrada se pudo votar en Menéame.
Nota 2: Esta entrada ha llegado al Olimpo en Divoblogger.
Imagen: Javier Lastras en Wikimedia Commons.






Deja una respuesta