Se acaba un año más. Un 2016 en el que no hemos podido leernos todo lo que me gustaría, entre nuevas líneas de investigación, más clases de lo esperado y algún apoyo menos de lo esperado. Pero aquí estoy, un año más, para desearos a todos un estupendo 2017 y, de paso, aprender algo nuevo.
Probablemente ya conoces lo que son los poliominós; objetos geométricos en 2D que se obtienen pegando cuadrados por alguno de sus lados. Como ejemplo, éstas son las posibilidades que tienes usando, respectivamente, 1, 2 o 3 cuadrados:
Si te fijas en los 6 poliominós de tamaño 3, verás que en realidad algunos se pueden conseguir rotando otros (por ejemplo, la barra horizontal se puede obtener rotando la barra vertical) pero no se puede conseguir uno haciendo una traslación de otro. A este tipo de poliominós se les llama poliominós fijos, pero también hay otras definiciones de poliominó.
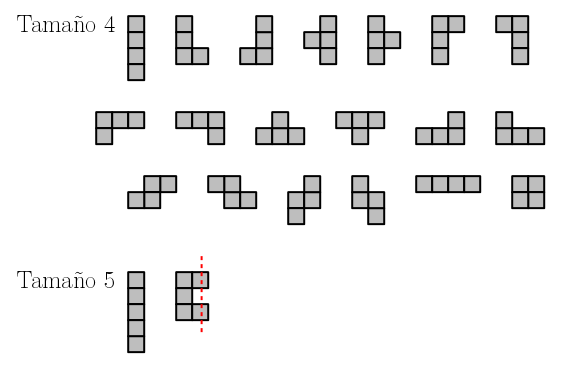
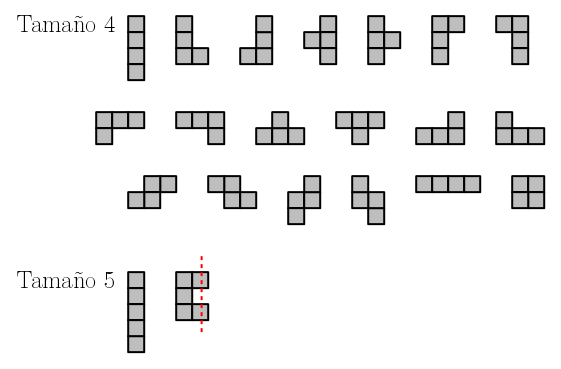
Ahora que ya los conocemos mejor, podemos dibujar los 19 poliominós de tamaño 4. Incluso podríamos animarnos a dibujar los 63 poliominós de tamaño 5…
…pero me he parado al dibujar el segundo. Como puedes ver, para éste hay una recta vertical que lo corta, lo deja de cortar, y lo vuelve a cortar. Eso lo distingue de todos los anteriores, porque hasta este último, cualquier recta vertical cortaba al poliominó «una única vez» (más técnicamente, en una única componente conexa).
A los poliominós a los que les pasa esto se les llama convexos por columnas y, como ves, hasta tamaño 4 todos lo son. Para tamaño 5 es fácil convencerse de que solo hay dos poliominós que no son convexos por columnas; el de la figura y su simétrico.
Así, el número de poliominós (fijos) convexos por columnas es:
- 1 de tamaño 1.
- 2 de tamaño 2.
- 6 de tamaño 3.
- 19 de tamaño 4.
- 61 de tamaño 5.
Y si introducimos estos números en la Enciclopedia On-Line de Secuencias de Números Enteros, obtenemos como segundo resultado lo que estamos buscando; la secuencia A001169 nos da el número de poliominós fijos convexos por columna para cada tamaño (también llamados «board-pile polyominoes»):
- 196 de tamaño 6.
- 629 de tamaño 7…
…¡¡Y para tamaño 8 hay exactamente 2017 poliominós fijos que son convexos por columnas!!
Ésta es una propiedad muy especial, porque el anterior número que la cumple es el 629 y el siguiente número que la cumple es el 6466, así que ninguno de nosotros ha vivido ni volverá a vivir un año con esta propiedad. Disfrútalo, y
¡¡Que tengas un muy feliz año 2017!!
Para saber más:
Si no los conocías, seguro que los poliominós te han recordado al famoso juego del Tetris; te recomiendo esta entrada de Raúl Ibáñez en el Cuaderno de Cultura Científica para aprender más al respecto.
Puedes ver algún otro ejemplo de poliominó convexo por columnas en la entrada de Wolfram Mathworld, donde también podrás ver que el número de poliominós fijos convexos por columnas cumple (para tamaño n a partir de 5) la relación de recurrencia a(n) = 5*a(n-1) – 7*a(n-2) + 4*a(n-3). Puedes encontrar una interesante demostración de esta recurrencia (para convexo por filas, cuyo número es el mismo) en este artículo de Dean Hickerson.
ACTUALIZADO: También puedes encontrar los 629 poliominós de tamaño 7 convexos por filas en esta entrada (en japonés).
Otra propiedad interesante del número 2017 es que coincide con el número de trozos en que quedaría cortada una pizza si se le hicieran 63 cortes en línea recta (sin tres cortes concurrentes en un solo punto). Esto se conoce como la secuencia del cortador perezoso o, más formalmente, como la secuencia de números poligonales centrales.
Estos números aparecen en la secuencia A000124 de la enciclopedia y el 2017 es el término 63 (si empezamos a contar en 1). La secuencia A055469 contiene los términos de la anterior que, además, son un número primo. Como el 2017 es primo, aparece también en esta secuencia, y lo hace en el lugar 21.
Nota: Esta entrada participa en la Edición 7.9 del Carnaval de Matemáticas, que en esta ocasión organiza el blog de José Luis Muñoz.

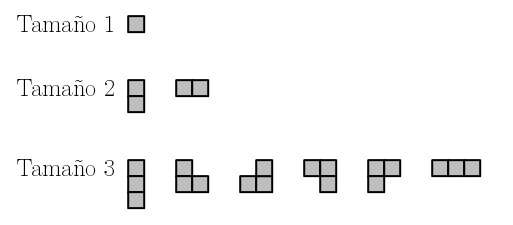


Deja una respuesta