Reconócelo, tu mesa es un caos. Un caos más o menos controlado en el que papeles, bolígrafos y lápices de colores conviven en frágil armonía. Quizá no tengas tiempo para pararte a pensarlo (y puede que menos aún para leer esta entrada), pero en ese desorden también hay matemáticas. ¿Qué te parece si las matemáticas te ayudan a justificar ese desorden, aprendiendo lo que es un grafo «light»?
Es probable que en estos días de junio tu mesa se parezca un poco a esto:
Quizá sea porque estás de exámenes, o quizá porque ya los has terminado y tienes mejores cosas que hacer antes de recoger tu mesa ;-). También puede que ya no seas estudiante y tengas así la mesa mientras suspiras por el verano y recuerdas, con una mezcla de ternura y alivio, aquellos años de exámenes y vacaciones de más de un mes.
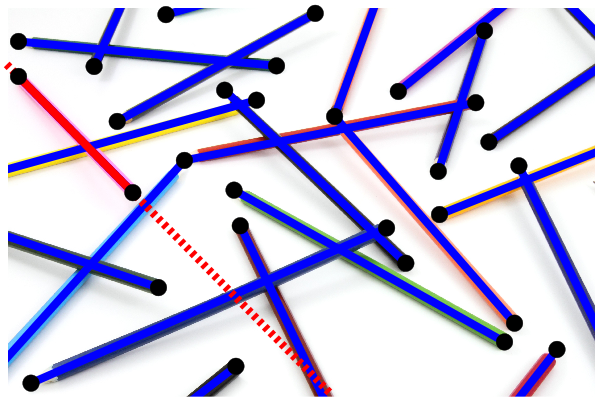
Cualquier excusa es buena para aprender, así que hoy vamos a buscar matemáticas en este desorden y, de paso, darte una excusa para justificarlo ante tu madre o tu jefe :-). Si te pones las gafas matemáticas (para los despistados; se puede pinchar en el enlace), dejarás de ver bolígrafos, lápices y rotuladores, y empezarás a ver puntos y segmentos:
Ahora hay que ver qué podemos hacer con estos puntos y segmentos. Por ejemplo, puedes contar el número de veces que un segmento se cruza con otro, como ya hicimos en una entrada anterior. Pero si quieres aprender algo nuevo, te propongo investigar si el desorden de tu mesa forma o no un grafo «light» (que traduciremos como grafo ligero). ¿Quieres saber lo que es eso?
Cada segmento puedes prolongarlo a una recta, que dividirá tu mesa en dos partes, llamadas lados del segmento:
Para el segmento rojo de esta figura tenemos el lado de «arriba a la derecha» y el lado de «abajo a la izquierda». Para que no haya discusión, la recta se queda aparte, es decir, no está incluida en ninguno de los dos lados.
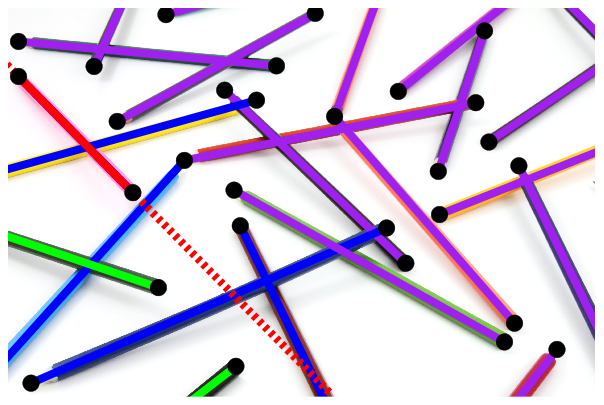
Lo siguiente va a ser mirar dentro de cada uno de esos lados en que ha quedado dividida tu mesa, buscando segmentos que estén (totalmente) contenidos en ese lado. En nuestro ejemplo, el lado de «abajo a la izquierda» tiene 2 segmentos, marcados con color verde, y el lado de «arriba a la derecha» tiene 16 segmentos, marcados con color violeta:
Para hacerlo más entretenido, y como estamos en tiempo de operación bikini (vale, vale, quizá ya sea tarde para eso… pero no hay que perder la esperanza), vamos a contar calorías. En la figura anterior el lado de «arriba a la izquierda» tiene 16 calorías (segmentos) y el lado de «abajo a la derecha» tiene sólo 2 calorías (segmentos). Entonces tiene todo el sentido del mundo decir que un lado es «light» (mejor vamos a llamarlo «ligero») cuando no tiene calorías, es decir:
Un lado de un segmento es un lado ligero cuando no contiene ningún segmento.
En la siguiente figura, el lado de «arriba a la izquierda» es un lado ligero (no tiene calorías), mientras que el de «abajo a la derecha» no es ligero (tiene más calorías que un refresco azucarado):
Y ahora que ya sabes lo que es un lado ligero, la definición de segmento ligero te resultará bastante natural:
Un segmento es un segmento ligero cuando alguno de sus dos lados es ligero (es decir, no contiene segmentos).
Es importante darse cuenta de que no hace falta que los dos lados sean ligeros, sino que basta con que lo sea uno de ellos. Así, el segmento rojo de esta última figura es ligero aunque el lado de «abajo a la derecha» no lo sea (tenía un montón de calorías). Sin embargo, el segmento rojo de la figura anterior a ésta no es ligero, porque sus dos lados contenían segmentos (un lado 2 y el otro 16).
Y ya estás llegando a la meta. ¿Qué crees que va a ser un grafo ligero? ¡¡Bingo!!
Un conjunto de puntos y segmentos entre ellos es un grafo ligero cuando todos los segmentos son ligeros (es decir, tienen un lado que no contiene otros segmentos).
O sea, que un grafo es «light» cuando todos sus segmentos tienen un lado sin calorías.
El grafo de los lápices de colores que teníamos antes no es ligero, porque ya vimos que había un segmento para el que ninguno de los lados era ligero (uno contenía 2 calorías, los segmentos verdes, y el otro 16 calorías, los segmentos morados).
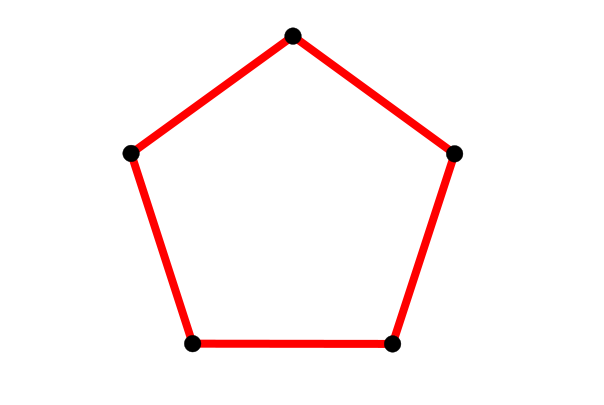
Sin embargo, el grafo de un polígono convexo sí que es un grafo ligero; para cada segmento el lado hacia el exterior del polígono nunca contiene ningún otro segmento, así que no tiene calorías y por tanto siempre es ligero.
¡Hala! A seguir aprendiendo (con las calorías mejor no obsesionarse).
Puedes seguirnos en Twitter, Facebook y Google+.
Imagen de los lápices de colores: PublicDomainPictures en Pixabay.
Para saber más:
En las figuras de los lápices de colores, hay segmentos que terminan en el borde de la imagen. A la hora de contarlos o no en un lado, los he tenido en cuenta como si tuvieran otro punto en su intersección con el borde de la imagen (aunque he preferido no dibujar esos puntos).
Esta entrada está basada en la entrada Always look on the light side of graphs, que escribí para Mapping Ignorance. Si no conoces ese blog de divulgación científica, te invito a que le eches un vistazo.
Lo habitual es considerar que los puntos están en posición general, es decir, que no hay tres puntos sobre una misma recta. En ese caso, tiene sentido preguntarse ¿cuántos segmentos puede haber en un grafo ligero? Algunos investigadores han trabajado en esta cuestión; Eyal Ackerman, Jacob Fox y Rom Pinchasi han demostrado recientemente que el número de segmentos en un grafo ligero es como mucho 16 veces el número de puntos, es decir:
Un grafo ligero con (n) puntos tiene como mucho (16 n) segmentos.
La noción de grafo ligero puede generalizarse a la de grafo (k)-ligero. En lugar de pedir que los lados no contengan ningún segmento, se es un poco más flexible (no se es tan riguroso con las calorías) y se admite que contengan hasta (k) segmentos. Para este problema, los mismos autores demuestran que:
Un grafo (k)-ligero con (n) puntos tiene como mucho (24sqrt{3}sqrt{k} n) segmentos.
También demuestran que asintóticamente (cuando el número (n) de puntos tiende a infinito), esta cota (O(sqrt{k}n)) es la mejor posible.
En la entrada de Mapping Ignorance puedes ver cómo este problema está relacionado con el de los segmentos elusivos, en el que también han trabajado otros grupos de investigadores.






Deja una respuesta