Si juegas al póquer seguro que has leído artículos con fórmulas para calcular qué probabilidades tienes de ganar. Si no juegas, quizá te interese saber qué fórmulas son ésas. En cualquiera de los dos casos, deberías saber de dónde salen esas fórmulas y hasta qué punto puedes fiarte de ellas. A la hora de jugar siempre pueden venir bien algunos consejos.
Introducción
El póquer surgió en el siglo XIX y actualmente es uno de los juegos de cartas más importantes y más jugados en los casinos de todo el mundo. Hay varios estilos de juego, pero hoy vamos a centrarnos en el estilo Texas Hold’em (sin límites).
Las reglas son muy sencillas: se trata de hacer la mejor mano de 5 cartas, teniendo nuestras dos cartas y las cinco cartas presentes en la mesa. Al principio se nos reparten dos cartas (pre-flop), luego se descubren tres (flop), luego la cuarta (turn) y después la quinta y última (river) siempre y cuando haya apuestas o se acuerda pasar en cada fase.
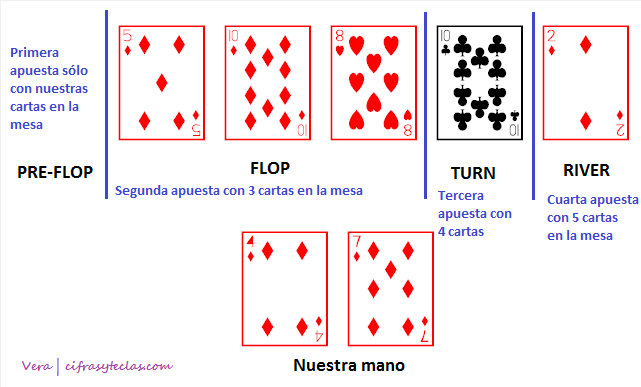
Con ello las combinaciones a hacer en orden creciente son: carta alta, pareja, doble pareja, trío, escalera, color, full house, póquer, escalera de color, escalera real de color.
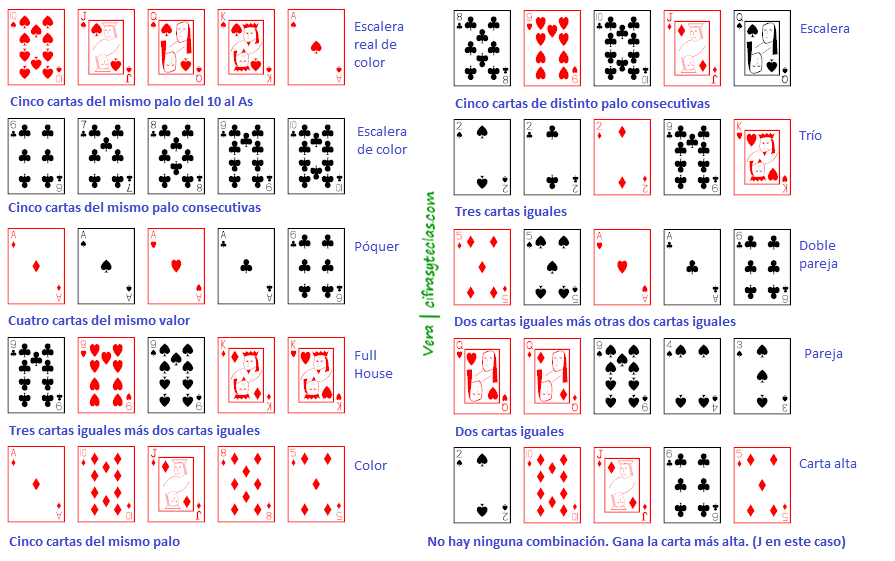
Dicho todo esto hay muchos jugadores profesionales que han escrito libros en los que podemos leer sus consejos a la hora de jugar, pero en esta entrada intentaré daros algunos de mis consejos (como aficionada 🙂 ), cosas que he ido aprendiendo con la práctica y donde me he dado cuenta de que a veces la probabilidad en este juego puede resultar muy engañosa, sobre todo cuando empiezas a jugar los primeros días.
Una fórmula y su explicación
Es bastante común enseñar a los principiantes una fórmula para calcular qué probabilidad hay de que la siguiente carta que salga sea la que tú necesitas para hacer una buena mano. De esa forma puedes decidir si sigues apostando o te retiras.
Se trata de contar outs y como resumen podemos decir que se trata de «contar las cartas que aún no han salido y que sirven para mejorar nuestra mano». Un ejemplo bastante común: Si tenemos en nuestra mano dos cartas del mismo palo y en el flop hay también dos cartas del mismo palo, ¿qué probabilidad existe que salga la siguiente carta del mismo palo para así poder hacer color? La fórmula dice que tienes que hacer el siguiente cálculo:
- De las 13 cartas posibles del mismo palo que hay en la baraja, tienes 2 y en la mesa hay otras 2, por lo que pueden quedar 9 cartas del mismo palo en la baraja [ 13-4=9. ]
- Si estás después del flop: Te quedan el turn y el river. Para calcular la probabilidad de que la carta deseada salga en el turn o el river tienes que multiplicar por 4 el número del primer punto [9cdot 4=36%.]
- Si estás después del turn: Sólo te queda el river. Para calcular la probabilidad de que la carta deseada salga en el river tienes que multiplicar por 2 el número del primer punto [9cdot 2 = 18%.]
Y en función de esto tú decides si seguir apostando o retirarte.
La pregunta es ¿de dónde sale esa fórmula? Y la respuesta te va a resultar sorprendente.
Para empezar, recuerda que la probabilidad de que ocurra un suceso A es:
[p(A)=frac{mbox{casos favorables}}{mbox{casos posibles}}]
Ahora vamos a analizar los dos casos anteriores:
- Si estás después del turn:
Conocemos 6 cartas (las tres del flop, la del turn y nuestras dos cartas), por lo que hay 52-6=46 cartas que desconocemos (suceso A). Si hay (x) cartas que nos sirven para completar una buena mano, observando la fórmula de un suceso podemos deducir que la probabilidad de que en el river salga una carta que no nos vale para completar una buena mano se expresa de la siguiente forma:
[frac{46-x}{46}.]
Por lo que la probabilidad de que salga una carta que sí nos vale es la probabilidad total menos la anterior:
[1-frac{46-x}{46}.]
Entonces, ¿por qué la fórmula dice que multipliques por 2, es decir, que uses la función (2cdot x)? Lo verás en cuanto dibujemos ambas funciones:
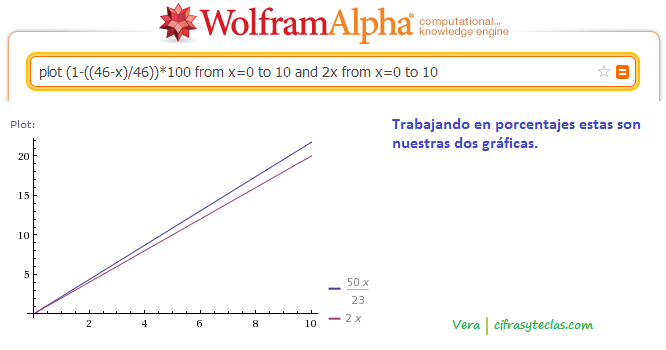
Como ves, la función (2cdot x) es una aproximación razonable a la función de verdad, sobre todo para valores pequeños de (x), que suele ser lo habitual, ¡¡y es mucho más fácil de recordar!!
- Si estás después del flop:
En este caso conocemos 5 cartas (las tres del flop y las dos nuestras). En la baraja hay 52, por lo que desconocemos 52-5=47 cartas que pueden salir en el turn (suceso A), y 47-1=46 cartas que saldrán en el river (suceso B). De nuevo vamos a usar la fórmula de un suceso y ahora también vamos a usar que la probabilidad de que ocurran dos sucesos independientes es el producto de las probabilidades de éstos.
Si hay (x) cartas que nos sirven para completar una buena mano, podemos expresar la probabilidad de que tanto en el turn como en el river salgan cartas que no nos valen para completar una buena mano como:
[frac{47-x}{47}cdotfrac{46-x}{46}.]
Por lo que la probabilidad de que en alguno de ellos salga una carta que sí nos vale para hacer una buena mano es la total menos la anterior:
[1 – frac{47-x}{47}cdotfrac{46-x}{46}.]
Recuerda que en este caso la fórmula dice que multipliques por 4, es decir, que uses la función (4cdot x). La explicación vuelve a estar clara si dibujamos ambas funciones:
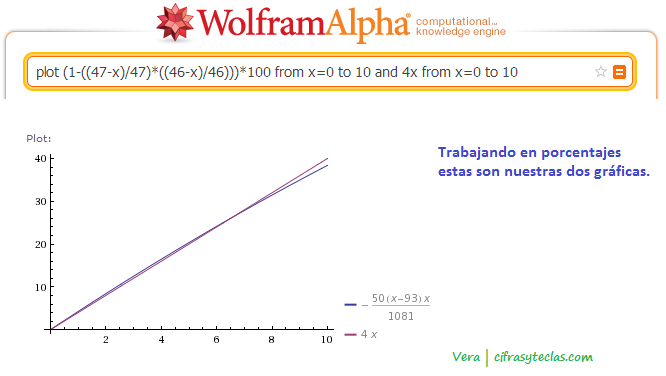
Por qué no hay que seguir ciegamente la fórmula
Después de contar esta fórmula y explicar de dónde viene, deciros que en mi opinión, este cálculo nos puede inducir a error y engaño. Veamos un ejemplo:
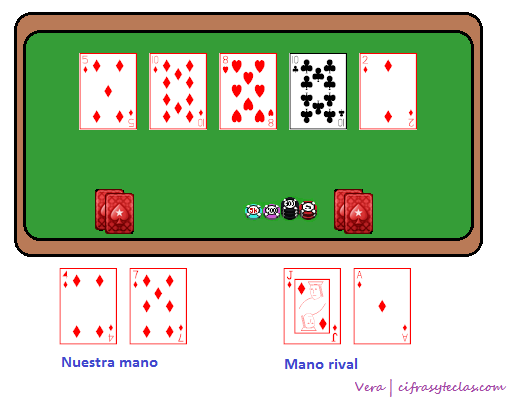
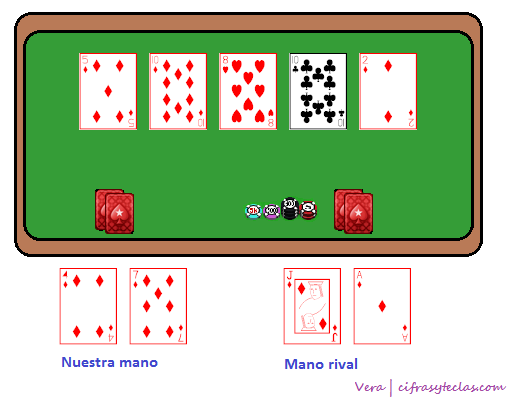
Tenemos en nuestra mano 4♦ y 7♦. Como todas las cartas tienen la misma probabilidad de salir, podemos pensar que tenemos una buena mano (realmente esta mano no es tan mala del todo). Dos cartas del mismo palo, y puede ser también un proyecto de escalera, por lo que apostamos.
Después del river tenemos las siguientes cartas: 5♦ 10♦ 8♥ 10♣ 2♦. Cuando estás justo después del flop sólo conoces las tres primeras de estas cartas y ves que:
- Para tener escalera necesitaríamos un 6 en alguna de las dos últimas cartas (con lo que obtendríamos 4,5,6,7,8). Hay cuatro cartas con el número 6 y no tienes a la vista ninguna de ellas, así que la fórmula dice que la probabilidad es (4cdot 4=16%).
-
Para tener color necesitaríamos otra carta de rombos en alguna de las dos últimas cartas. Tienes a la vista 4 cartas de rombos del total de 13 que hay (recuerda que las dos últimas cartas no las has visto todavía). Y en el cálculo anterior hemos contado el 6 de rombos que nos sirve para hacer escalera. Por tanto, pueden quedar
13-4=913-5=8 cartas que te sirven. Por tanto, la fórmula dice que la probabilidad es4·9 =36%(4cdot 8=32%).
Así que tenemos un 36% + 16% = 52% 32% + 16% = 48% de hacer una buena mano. Como un 52% 48% es un buen porcentaje para arriesgar, lo hacemos. Finalmente, después de que salen todas las cartas, tenemos color al 10. Nuestro oponente nos descubre su mano: J♦ y A♦. Gana nuestro contrincante, ya que tiene color al as:
Con este ejemplo quiero explicar por qué no hay que jugar todas las manos, ya que las personas que empiezan a jugar suelen apostar con todas las manos (yo lo hice 🙂 ). Los jugadores expertos suelen apostar con manos buenas y altas, tirando las manos malas, por lo que rara vez cuando les veamos jugar en la televisión les veremos apostar con 4♦ y 7♦. Pueden hacerlo si las ciegas son muy grandes y si no hay muchos jugadores en la mesa, o si conocen bien como juega un jugador concreto.
Otro tema que podría ser interesante es ir haciendo un muestreo mentalmente de las cartas que van saliendo, puede que así cuando estemos indecisos entre si apostar o no esto nos ayude. Puede parecer una tontería ya que todas las cartas tienen la misma probabilidad de salir, pero nos puede servir de ayuda cuando no sepamos bien qué hacer.
Algunos consejos
Por último me gustaría dar algunos de los consejos que he ido aprendiendo con el tiempo para que pocas veces nos pase como en el ejemplo anterior:
- Cuando estemos jugando observar como juegan los demás jugadores, si alguien les iguala las apuestas observar las cartas que tienen; esto nos hará saber más o menos con qué cartas suele jugar y puede ser una buena pista para saber que cartas se pueden apostar contra el.
- Intentar no jugar siempre con el mismo patrón; como por ejemplo, si apostamos en el preflop y si cuando sale el flop vemos que nuestras cartas no ligan, retirarnos, y si vemos que nuestras cartas ligan seguir apostando una buena cantidad de fichas. Si siempre hacemos esa jugada los demás jugadores se darán cuenta de nuestro estilo de juego y les será ganarnos fácilmente.
- Observar la posición en la mesa de los jugadores cuando hacen la apuesta. Si están en las primeras posiciones desconfiar, si están en las últimas «podemos intentar jugar con cuidado».
- Tener el mismo patrón de apuestas y no ir apostando una cantidad pequeña cuando intentamos hacer un farol y cantidades grandes cuando tenemos buenas cartas.
- En general, tirar manos bajas, apostar con manos altas, y si las ciegas o apuestas son pequeñas ver el flop con manos intermedias.
- Hacer pocos faroles.
- Cuidado con la gente que pasa, pasar NO significa no tener nada.
- Tener cuidado si queremos ligar una escalera, pareja, doble pareja o color cuando en la mesa hay cartas mayores que las que tenemos en nuestra mano.
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Nota 1: Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas, cuyo anfitrión es este humilde blog.
Nota 2: Esta entrada ha llegado a portada en Menéame. ¡Gracias!
Nota 3: Cometí un error en el cálculo contado el 6♦ dos veces. Me disculpo, y arreglo el error.


Deja una respuesta