Tengo un amigo, de ésos que no han pasado por la universidad pero van sobrados de curiosidad, que durante un tiempo cada vez que nos veíamos me preguntaba «A ver, matemático, ¿cuánto son 2+2?» a lo que yo respondía «Pues depende, cuando tengamos un rato te lo cuento». Siempre teníamos algo mejor que hacer y nunca llegué a contárselo, así que voy a hacerlo ahora. Me juego una ronda a que lo entiende, y seguro que tú también.
Si te estás preguntando cómo es posible que 2+2 no sea 4 es porque conoces los números naturales y sabes cómo sumarlos (y muchas cosas más). Con esos números y esa suma nadie duda de que 2+2 sea 4, ¿verdad? Así que para tener un resultado distinto vamos a necesitar otros ingredientes. En particular vamos a trabajar con cuerpos finitos (que no son lo que estás pensando). Pero no te asustes, verás cómo no hacen falta ingredientes muy sofisticados.
Nos bastará con el calendario que tengo en mi mesa. Vamos a empezar con esta imagen:
Fíjate en los días de la semana. Si estás a lunes y avanzas dos días, está claro que llegas al miércoles, ¿verdad?
Ahora fíjate en los números que hay debajo de cada día de la semana. El ejemplo de antes nos dice que 1+2=3, ¿a que sí?
Vamos con otro ejemplo. Si estás a viernes y avanzas tres días, ¿a qué día llegas?
Pues se te ha pasado volando el fin de semana y has llegado al lunes, ¿verdad? Ahora fíjate otra vez en los números…
¿¿Me estás diciendo que 5+3=1??
Pues sí, resulta que 5+3=1 en el mundo de las semanas de 7 días. Ahora puedes buscar a alguien con quien jugarte una ronda e invitarle al mundo de las semanas de 3 días (por ejemplo viernes, sábado y domingo ;-)).
¿Cuánto son aquí 2+2?
¡¡¡¡Tacháááánnnn!!! Ahora 2+2 ya no es 4 sino 1 (de hecho, en este mundo no existe el 4) y nos hemos ganado una ronda. ¡A disfrutar!
Para saber un poco más:
Esos mundos de las semanas de 7 ó 3 días no son tan raros como puede parecerte. Se llaman cuerpos finitos y, aunque no lo supieras, los estás utilizando todos los días. Son cruciales en criptografía y en teoría de códigos, así que es muy probable que los estés usando al conectarte a una web segura, hacer pagos electrónicos o escuchar música en formato digital. Imagínate cómo será que hasta hay una revista científica dedicada a publicar nuevos resultados sobre cuerpos finitos y sus aplicaciones.
Una de sus ventajas es, precisamente, ser un cuerpo. De manera informal, eso significa que sus elementos se pueden sumar, restar, multiplicar y dividir con las propiedades habituales. Sí, has leído bien, también se puede restar, multiplicar y dividir. ¿Quieres saber cómo?
Vamos a centrarnos en el mundo de las semanas de 7 días, que ahora ya sabes que en realidad es el cuerpo finito con 7 elementos, al que llamaremos (mathbb{F}_7).
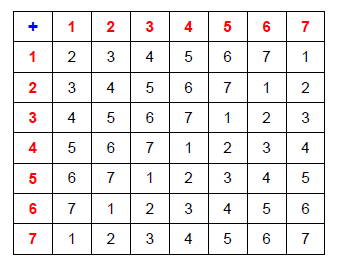
Ya sabes cómo sumar en (mathbb{F}_7); antes has visto que 1+2=3 y que 5+3=1 y, de manera similar, puedes comprobar todas las sumas posibles. Como lleva un rato, te he puesto los resultados en esta tabla:
Para saber el resultado de cualquier suma basta colocarse en la fila y la columna correspondientes. Por ejemplo, 6+5=4 (también puedes mirar el calendario para comprobar que si estás en el sexto día de la semana, sábado, y avanzas cinco días llegas al cuarto día, jueves). Esta suma es un poco distinta de la que ya conocías para los números naturales, pero cumple las mismas propiedades. Por ejemplo, es interesante que compruebes en la tabla que:
- La primera fila es igual que la primera columna, la segunda fila es igual que la segunda columna… y así todas. Eso significa que la suma es conmutativa.
- La fila del 7 es igual que la fila superior o, en otras palabras, sumar 7 a cualquier número da como resultado ese mismo número. Eso significa que el 7 es el elemento neutro para la suma (el análogo al 0).
- En cada fila hay un 7 o, en otras palabras, para cada número de (mathbb{F}_7) se puede encontrar la solución de
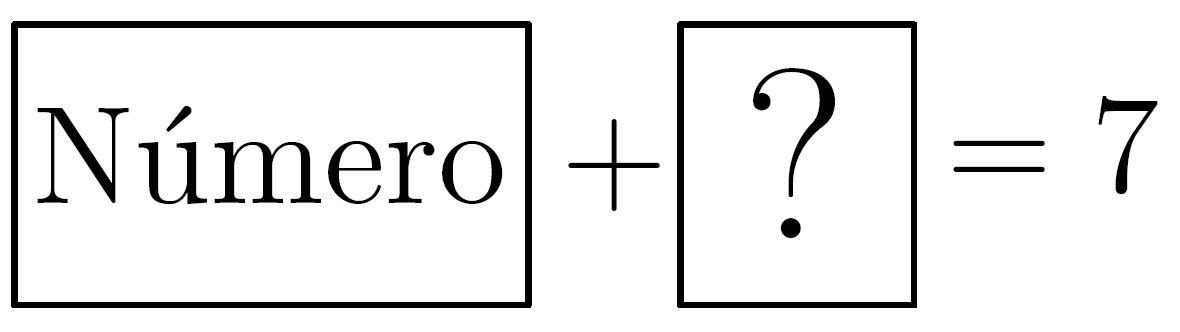 Eso significa que cada número tiene un opuesto. Por ejemplo, el opuesto de 2 es 5 porque 2+5=7 y, si no te asusta, puedes escribir que -2=5 (recuerda que el 7 es el análogo al 0).
Eso significa que cada número tiene un opuesto. Por ejemplo, el opuesto de 2 es 5 porque 2+5=7 y, si no te asusta, puedes escribir que -2=5 (recuerda que el 7 es el análogo al 0).
Y ahora que ha aparecido un signo -, parece que toca aprender a restar en (mathbb{F}_7), ¿no? Quizá lo más fácil sea pensar que restar no es más que «sumar hacia el otro lado»; si miramos otra vez el calendario y calculamos 6-2
sin sorpresas, comprobamos que 6-2=4. Otra manera de hacerlo es usar el elemento opuesto;
[6-2=6+(color{red}{-2})stackrel{mbox{Antes}}{=}6+color{red}{5}stackrel{mbox{Tabla}}{=}4.]
¿Te atreves ahora a calcular 3-5? Piénsalo un poco antes de seguir leyendo…
¡Resulta que 3-5=5 en (mathbb{F}_7)! Si quieres, puedes hacer también la tabla con las restas en (mathbb{F}_7), pero esto ya nos está quedando un poquito largo así que, si te parece, vamos a pasar a la multiplicación :-).
Una vez que sabes sumar, también sabes multiplicar… porque al fin y al cabo multiplicar es sumar varias veces, ¿verdad? Por ejemplo,
[4cdot 3=4+4+4=(color{red}{4+4})+4stackrel{mbox{Tabla}}{=}color{red}{1}+4stackrel{mbox{Tabla}}{=}5.]
Fácil, ¿no?
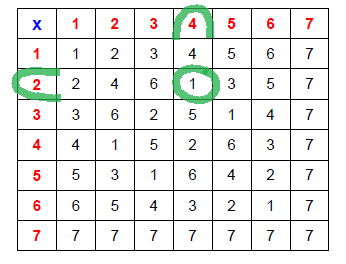
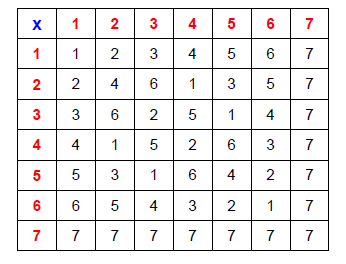
Igual que antes, podemos calcular todas las multiplicaciones posibles y tendremos la tabla de multiplicar de (mathbb{F}_7):
Esta tabla de multiplicar es un poco distinta de la que te aprendiste en el colegio, pero también cumple las propiedades habituales y es interesante que compruebes que:
- La primera fila es igual que la primera columna, la segunda fila es igual que la segunda columna… y así todas. Eso significa que el producto es conmutativo.
- La fila del 1 es igual que la fila superior o, en otras palabras, multiplicar por 1 a cualquier número da como resultado ese mismo número. Eso significa que el 1 es el elemento neutro para la multiplicación.
- En la última fila todos los números son 7 o, en otras palabras, multiplicar por 7 a cualquier número da como resultado 7 (y todo encaja, porque el 7 era el 0 de (mathbb{F}_7) y multiplicar por 0 debería dar como resultado 0).
- En todas las filas salvo la del 7 hay un 1 o, en otras palabras, para cada número de (mathbb{F}_7) salvo el 7 (que era el 0) se puede encontrar la solución de
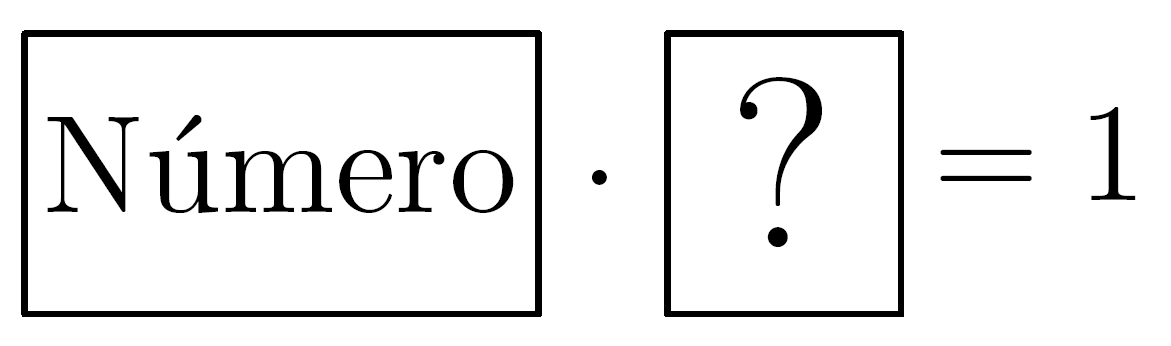 Eso significa que para cada número, salvo el 7, hay un inverso. Por ejemplo, para calcular el inverso de 2 buscamos la solución de
Eso significa que para cada número, salvo el 7, hay un inverso. Por ejemplo, para calcular el inverso de 2 buscamos la solución de
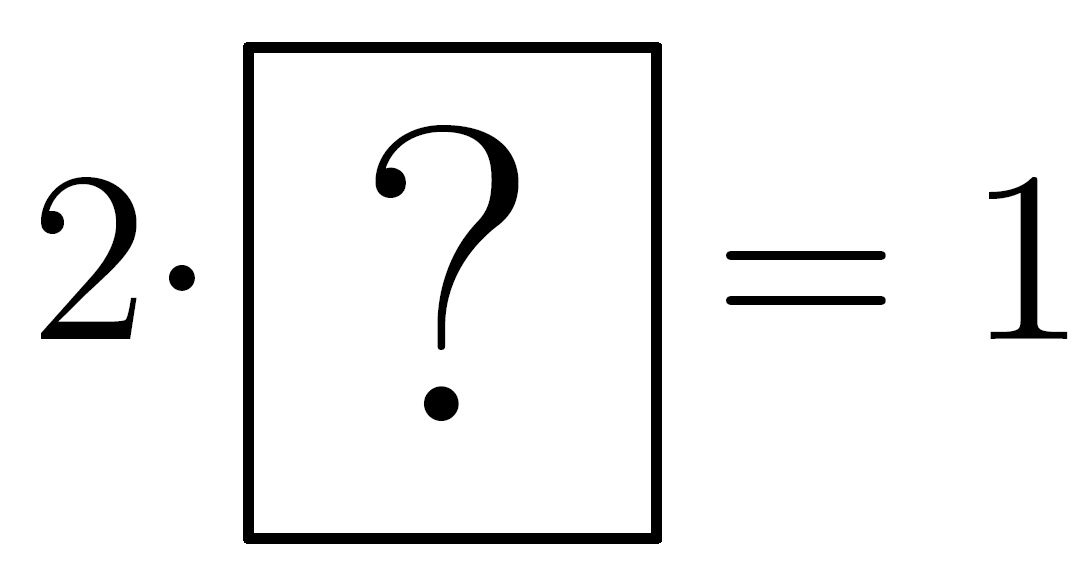 y mirando en la tabla comprobamos que 2·4=1
y mirando en la tabla comprobamos que 2·4=1
 Así que el inverso de 2 es 4 y, si no te asusta, puedes escribir que 1/2=4. Recuerda que el que no tiene inverso es el 7, que era el análogo al 0.
Así que el inverso de 2 es 4 y, si no te asusta, puedes escribir que 1/2=4. Recuerda que el que no tiene inverso es el 7, que era el análogo al 0.
Y si ha aparecido un signo ([/latex], ahora nos toca aprender a dividir en (mathbb{F}_7). Antes de hacerlo, date cuenta de que con los números naturales no siempre se puede dividir; por ejemplo 1/2 no es un número natural (sino racional). ¡¡Pero resulta que en (mathbb{F}_7) sí se puede dividir!! (y ésa es una de las claves de la utilidad de los cuerpos finitos).
Para aprender a dividir en (mathbb{F}_7) puedes pensar que «una división en realidad es una multiplicación por el inverso». Por ejemplo, 5/2 es en realidad 5·(1/2). Como ya hemos visto que 1/2=4, en (mathbb{F}_7) tendremos que
[5/2=5cdot (color{red}{1/2})stackrel{mbox{Antes}}{=}5cdotcolor{red}{4}stackrel{mbox{Tabla}}{=}6.]
Y de manera análoga podríamos hacer la tabla con todas las posibles divisiones… pero bastante tendrás con haber leído hasta aquí. ¡Enhorabuena! 🙂
Puedes seguirnos en Twitter, Facebook y Google +.
Nota 1: Aquí tienes las tablas de sumar y multiplicar para los números del 1 al 7. Si te animas a hacer alguna tabla para los números del 1 al que tú quieras, nos haría mucha ilusión que nos la enviaras (como una imagen) a cifrasyteclas@km77.com. Como en otras entradas, haremos una galería con vuestros envíos.
Nota 2: Esta entrada participa en la edición 4.1 del Carnaval de Matemáticas, cuyo blog anfitrión es Tito Eliatron Dixit.
Nota 3: Esta entrada ha llegado a portada en Menéame.
Nota 4: Esta entrada ha llegado a portada en Divúlgame.
Para saber todavía más:
Sólo puede haber cuerpos finitos con (p^r) elementos, donde (p) es un número primo y (rgeq 1) entero. Y al revés, para cada (p^r) así se puede construir un cuerpo finito con ese número de elementos. Por ejemplo, puedes leer por qué en Planet Math.
También puedes leer por qué para los números naturales 2+2 son 4, muy bien explicado por Tito Eliatron.
Quizá te interese el curso «Descodificando álgebra» en Miríada X que, entre otras cosas, habla de cuerpos finitos y su uso en criptografía.
Si quieres saber más sobre criptografía, puede interesarte este curso en Coursera o alguna de las múltiples páginas al respecto, como este Taller de Criptografía.
Sobre códigos te recomiendo el libro Codificación de la información o el libro Information Theory, Inference, and Learning Algorithms (éste último gracias a un comentario de janderfield)
Si te va la electrónica, puedes mirar este Trabajo Fin de Máster sobre cómo implementar en hardware las operaciones en cuerpos finitos.
Otra aplicación de los cuerpos finitos es el diseño de experimentos en estadística, sobre lo que también puedes echar un vistazo a algún libro.
También aparecen cuerpos finitos en la generación de números pseudo-aleatorios; un problema que permite, por ejemplo, simular por ordenador los resultados de lanzar varias veces seguidas un dado.
Y por último, pero no menos importante, los cuerpos finitos están relacionados con la noción de congruencia, que trataremos con más calma en otra ocasión. Por ejemplo, para calcular 5+3 en (mathbb{F}_7) se puede hacer 5+3=8 y luego tomar el resto de dividir 8 entre 7, que es 1, para decir que 5+3=1. Para calcular 4·3 se puede hacer 4·3=12 y luego tomar el resto de dividir 12 entre 7, que es 5, para decir que 4·3=5 en (mathbb{F}_7). Date cuenta de que el resto de dividir 7 entre 7 es 0, lo que concuerda con que 7 sea el 0 de (mathbb{F}_7). Un libro muy interesante sobre teoría de números, incluyendo congruencias, es Elementary number theory and applications, de Kenneth H. Rosen.












Deja una respuesta