Si en un triángulo rectángulo te dan los catetos y te piden hallar la hipotenusa, seguro que enseguida te acuerdas del Teorema de Pitágoras. En teoría, el problema ya está resuelto. Pero ¿sabías que no todas las soluciones teóricas resultan viables en la práctica? ¿Sabes cómo calcula la hipotenusa tu ordenador?
Imagina que eres el jefe del departamento de I+D de una empresa (es posible que te cueste un poco imaginarlo). Imagina que la empresa tiene que resolver un problema y ha decidido pedir consejo a un matemático (si eres matemático, seguro que te cuesta mucho imaginarlo).
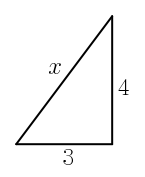
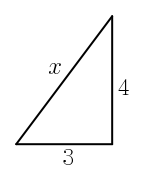
Envías a un ingeniero a contarle al matemático vuestro problema. Resulta que tu empresa tiene un triángulo rectángulo como éste
y necesita hallar la (x) como sea (pero no vale hacer el chiste fácil). El matemático enseguida propone usar el Teorema de Pitágoras
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
por el que (x^2=3^2+4^2) y por tanto [x=sqrt{3^2+4^2}=sqrt{9+16}=sqrt{25}=5.]
Entonces el ingeniero frunce el ceño y le dice al matemático que esa solución no sirve. Que las calculadoras de la empresa no admiten números más grandes que (5)… así que no van a poder calcular (3^2).
El matemático se queda un poco descolocado, nunca había pensado que pudiera hacer falta otra manera de calcular la hipotenusa. Pero el ingeniero le convence de que, si los datos sí caben en esas calculadoras (son (3) y (4)) y el resultado también (es (5)), tiene que haber alguna manera de poder hacer las cuentas.
Se ponen a trabajar juntos, cada uno aportando su manera de hacer las cosas y sus conocimientos. Además de pasárselo bien y aprender uno del otro, esta suma de esfuerzos no tarda en llevarles a encontrar una solución.
Entusiasmados, te llaman diciendo que ya lo han resuelto y que van a tu despacho para contarte cómo. Mientras llegan, dedicas un rato a ver si a ti se te ocurre alguna solución (éste es el momento, antes de seguir leyendo).
Cuando aparecen, el matemático se queda un momento mirando el suelo de tu despacho
mientras el ingeniero te propone ir haciendo las cuentas con una calculadora, para que compruebes que ningún resultado se pasa de (5):
- Divide el cateto más pequeño entre el más grande, es decir (3/4). Fíjate en que el resultado es como mucho (1) y por tanto cabe en tu calculadora.
- Eleva al cuadrado el resultado anterior, ((3/4)^2). El resultado de elevar al cuadrado algo que es como mucho (1) también es como mucho (1), así que también cabe en tu calculadora.
- Súmale (1) a lo anterior, (1+(3/4)^2). Como lo anterior era más pequeño que (1), este resultado es más pequeño que (2) y también cabe.
- Haz la raíz cuadrada de lo anterior, (sqrt{1+(3/4)^2}). Está claro que el resultado es más pequeño que lo de antes, así que sigue siendo más pequeño que (2) y cabe en tu calculadora.
- Multiplica lo anterior por el cateto más grande, (4cdotsqrt{1+(3/4)^2}). El resultado es el valor de (x) que estabas buscando, es decir, (5).
¡¡Es cierto!! No has necesitado utilizar ningún número más grande que (5).
Convencido de que la solución funciona, te aflojas un poco el nudo de la corbata y les cuentas al matemático y al ingeniero la verdad. En realidad, confiesas un poco avergonzado, la empresa pretende adelantarse a la competencia utilizando la calculadora de Google (que, de momento, sale gratis) para ser capaz de trabajar con números más grandes.
Hay un contrato muy importante que depende de poder hallar el valor de (x) en este triángulo:
Enseguida, el ingeniero te cuenta que el número más grande que cabe en la calculadora de Google (a día de hoy) es (1.7976931348623157cdot 10^{308}) y el matemático te dice que entonces tampoco se va a poder usar el Teorema de Pitágoras, porque con esa calculadora no se podrá calcular ((10^{155})^2=10^{310}).
Pero no te preocupes, te dicen a la par, la solución que han encontrado sigue funcionando. De nuevo te proponen que compruebes las cuentas, esta vez con la calculadora de Google:
- Divide el cateto más pequeño entre el más grande (10^{154}/10^{155}).
- Eleva al cuadrado el resultado anterior, ((10^{154}/10^{155})^2).
- Súmale (1) a lo anterior, (1+(10^{154}/10^{155})^2).
- Haz la raíz cuadrada de lo anterior, (sqrt{1+(10^{154}/10^{155})^2}).
- Multiplica lo anterior por el cateto más grande, (10^{155}cdot sqrt{1+(10^{154}/10^{155})^2}) y tendrás tu resultado.
El matemático y el ingeniero se van a la cafetería a seguir charlando mientras tú, encantado, subes a hablar con el director. Ojalá te dejara gastar dinero en estas cosas más a menudo…
Puedes seguirnos en Twitter, Facebook y Google +.
Nota 1: No habría apreciado del todo un ejemplo como el de esta entrada si no hubiera tenido la suerte de trabajar con ingenieros. Les estoy agradecido por ayudarme a abrir la mente y espero que esta entrada ayude a que los unos entiendan un poquito mejor a los otros 😉
Nota 2: Esta entrada ha resultado ganadora de la edición 4.12 del Carnaval de Matemáticas, cuyo blog anfitrión es High Ability Dimension.
Nota 3: Esta entrada ha llegado a portada en Menéame.
Nota 4: Esta entrada ha llegado a portada en Divúlgame.
Nota 5: Esta entrada ha llegado al Olimpo en Divoblogger.
Imagen central: Wikimedia Commons.
Para saber más:
En realidad, al calcular la hipotenusa de esta otra manera también estás usando el Teorema de Pitágoras. Si (h) es la hipotenusa, (c) es el cateto más pequeño y (C) el cateto más grande, lo que estás haciendo es
[Ccdotsqrt{1+left (frac{c}{C}right )^2}]
y eso te da la hipotenusa porque es igual a
[Ccdotsqrt{1+frac{c^2}{C^2}}=Ccdotsqrt{frac{C^2}{C^2}+frac{c^2}{C^2}}=Ccdotsqrt{frac{C^2+c^2}{C^2}}stackrel{mbox{Pitagoras}}{=}Ccdotsqrt{frac{h^2}{C^2}}=Ccdot{frac{h}{C}}=h.]
Esta entrada está inspirada en una de John D. Cook en su muy recomendable blog The Endeavour. Para saber cómo implementar en un ordenador el cálculo de la hipotenusa puedes leer la entrada sobre la función Hypot en Wikipedia.
Si te interesa saber por qué la calculadora de Google admite (1.7976931348623157cdot 10^{308}) como valor más alto, puedes consultar la entrada sobre precisión doble en coma flotante de la Wikipedia.
Si nunca te han explicado por qué es verdad el Teorema de Pitágoras, puedes ver este experimento en el que comprueban que se cumple, o leer esta entrada de Eulerianos al respecto. En esta otra página de José Manuel Arranz tienes alguna demostración más y, si te parecen pocas, puedes comprobar las 98 demostraciones del Teorema de Pitágoras en Cut The Knot.
Si te has quedado con la duda de por qué al matemático le parecía interesante el suelo de la sala de reuniones, puedes comprobarlo en esta entrada de Wikipedia sobre el enlosetado pitagórico.
Por desgracia, todavía se puede mejorar mucho la conexión entre la universidad y las empresas (en algunos países más que en otros), especialmente en lo relativo a matemáticas. Por eso me parece interesante destacar la gran labor de math-in (Red Española Matemática-Industria) e Itmati (Instituto Tecnológico de Matemática Industrial). Y si a algún científico, ingeniero o empresario le parece que puedo ser de alguna ayuda, aquí me tiene.


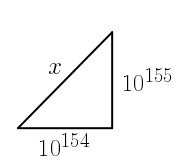

Deja una respuesta