Hace algunas entradas descubriste una figura geométrica que nunca te habían enseñado (aunque es muy sencilla de entender) el pseudo-triángulo. Si quieres jugar a unir puntos dibujando pseudo-triángulos y además ganar un premio, sólo tienes que seguir leyendo.

Es probable que ya recuerdes lo que es un pseudo-triángulo, porque esta figura geométrica ya apareció en una entrada anterior. Te habíamos propuesto descubrirlo jugando a unir puntos, con dos condiciones muy sencillas. En esta entrada vamos a añadir una tercera condición, también facilita, con la que podrás participar en el Décimo desafío Gaussianos-Guijarro y optar a llevarte un premio. Tú juegas a unir puntos, divirtiéndote mientras piensas, y te puedes llevar un premio. ¿Te apetece? No te asustes, porque no hace falta saber más matemáticas que las que vas a leer aquí.

Vamos con el juego. Imagina que tienes unos cuantos puntos en el plano, por ejemplo algo así:

Tu papel va a ser dibujar todas las uniones de puntos que puedas en línea recta (es decir, usando segmentos) teniendo cuidado de que se cumplan estas tres condiciones:

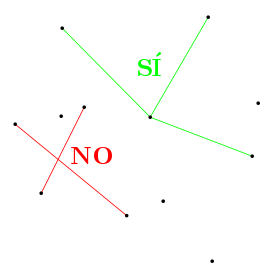
Condición 1: No puede haber cruces. Puedes pensar que esas líneas son cables que no se pueden cruzar.

Condición 2: En cada punto tiene que haber un ángulo de 180 grados sin ningún segmento. Puedes pensar que cada punto tiene que ser como el vértice de un abanico, con todos los segmentos saliendo de él hacia un lado y ninguno hacia el otro.

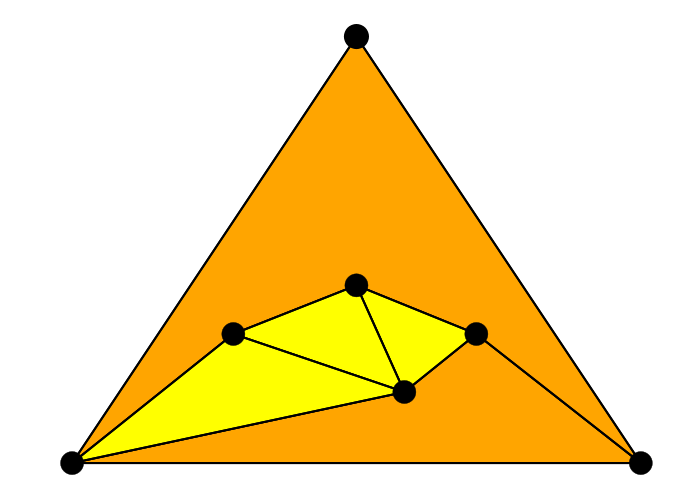
Cuando cumples las dos condiciones anteriores y ya no puedes dibujar más uniones, las figuras geométricas que aparecerán en tu dibujo serán algunos triángulos y otros pseudo-triángulos. A esto se le llama una pseudo-triangulación puntiaguda del conjunto de puntos. En este ejemplo los triángulos aparecen en amarillo y los demás pseudo-triángulos en naranja:

El borde de los triángulos siempre va a estar formado por tres lados, pero el borde de los pseudo-triángulos puede tener cualquier número de lados. En el ejemplo los hay de tres (triángulos), de cuatro (el pseudo-triángulo naranja de abajo) y de seis (el de arriba). La última condición tiene que ver con este número de lados:

Condición 3: Sólo puede haber pseudo-triángulos de tres lados (triángulos) y de cuatro lados (los pseudo-triángulos más pequeños que no son triángulos).

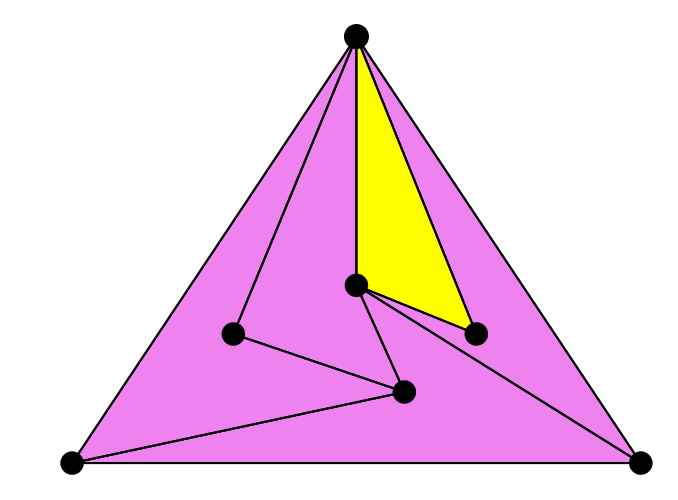
Éste sería un ejemplo para el conjunto de puntos anterior. Sólo hay un triángulo (en amarillo) y todo lo demás son pseudo-triángulos de cuatro lados (en morado):

Fíjate que en este ejemplo todos los puntos están dentro de un triángulo exterior, que los engloba a todos. (Pista: Cuando pasa esto, sólo puede haber un triángulo en el interior, el resto deben ser pseudo-triángulos de otro tipo). Ahora viene la primera pregunta que tienes que intentar responder:

Pregunta 1: Si tienes un conjunto (finito) de puntos dentro de un triángulo exterior, ¿siempre puedes conseguir pseudo-triangulación cumpliendo las tres condiciones anteriores?

O encuentras un conjunto de puntos para el que esto no se pueda hacer, o nos convences de que siempre se puede hacer (explicando cómo). Las respuestas no las mandes aquí, sino a la dirección de correo electrónico desafiosgyg (arroba) gmail (punto) com,  antes de que termine el domingo 29 de septiembre de 2013.

En el desafío tienes, además, otra pregunta. Imagina que tienes un conjunto de puntos dentro de un triángulo exterior, como antes, y has conseguido unirlos de manera que se cumplen las tres condiciones. En vez de colorear los triángulos y pseudo-triángulos, ahora vas a colorear los puntos. Pero tienes que hacerlo con una cuarta condición:

Condición 4: Colorea los puntos de manera que nunca aparezcan unidos dos puntos del mismo color.

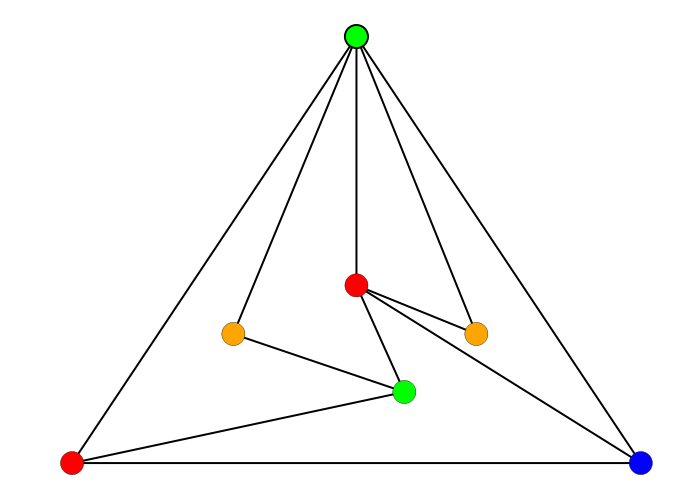Puedes comprobar que, efectivamente, no hay dos puntos del mismo color que estén unidos. En este ejemplo hemos usado cuatro colores (azul, rojo, naranja y verde). La segunda pregunta que tienes que responder es:

Pregunta 2: ¿Cuál es el menor número de colores con el que siempre vas a poder colorear los puntos cumpliendo la condición?

Primero puedes probar a ver si en este ejemplo puedes hacerlo con menos de cuatro, y después puedes intentar ver con cuántos colores podrías hacerlo en cualquier otro ejemplo.

En las dos preguntas puedes suponer, si quieres, que los puntos están en posición general (que no hay tres de ellos alineados). Como no hace falta saber muchas matemáticas, sólo jugar, pensar y tener un poco de ojo, cualquiera que lea esta entrada puede intentar resolver el problema y enviar su respuesta al correo electrónico desafiosgyg (arroba) gmail (punto) com,  antes de que termine el domingo 29 de septiembre de 2013. Seguro que a Gaussianos le gustará que participes… y a nosotros nos encantaría haberte ayudado a ganar 🙂

¡Ánimo!

Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.