En una entrada anterior proponíamos un juego sumando las cifras de tu matrícula. Ahora que ha pasado un tiempo prudencial, vamos a analizar los resultados y responder a las siguientes preguntas: ¿Cuántas veces ha aparecido cada raíz digital y cada persistencia aditiva en las matrículas que nos habéis enviado? ¿Cuántas veces era de esperar que apareciera cada una?
Vamos a empezar recordando de qué estamos hablando. En aquella entrada proponíamos calcular la raíz digital de tu matrícula. Para ello había que sumar todas sus cifras y, si el resultado tenía más de una cifra, volverlas a sumar… y así hasta obtener un resultado con una sola cifra, que es la raíz digital de tu matrícula. Por ejemplo:
[8483 stackrel{mbox{Suma}}{longrightarrow} 23 stackrel{mbox{Suma}}{longrightarrow} 5]
Así que (8483) tiene raíz digital (5). Además, de paso estabas calculando la persistencia aditiva de tu matrícula, que es el número de veces que hay que «sumar todas las cifras». En este caso, (8483) tiene persistencia aditiva (2).
Propusimos un cuestionario anónimo para hacer una muestra con las matrículas de nuestros lectores y, después de 77 matrículas, obtuvimos los siguientes resultados para la raíz digital:
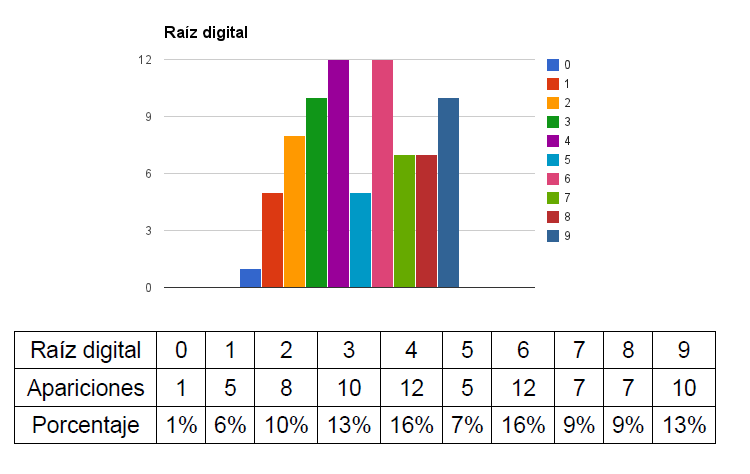
Y éstos otros para la persistencia aditiva:
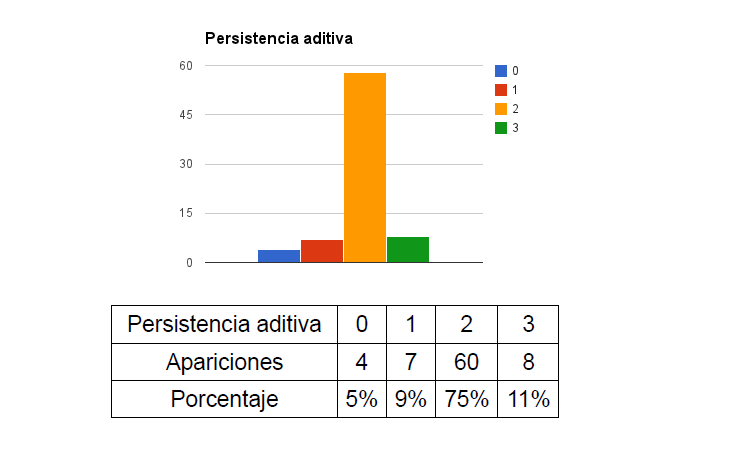
(En ambos casos los porcentajes están redondeados).
Hay que tener en cuenta que la muestra no es significativa, porque 77 matrículas son pocas para poder sacar conclusiones. Pero sí podemos preguntarnos ¿cuáles «deberían ser» los resultados? Para hacer más fácil el análisis vamos a centrarnos en el caso de las matrículas españolas, que tienen cuatro números, desde (0000) hasta (9999).
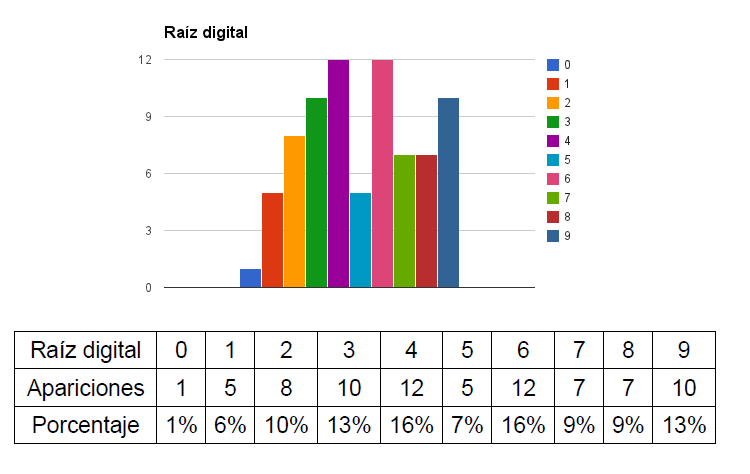
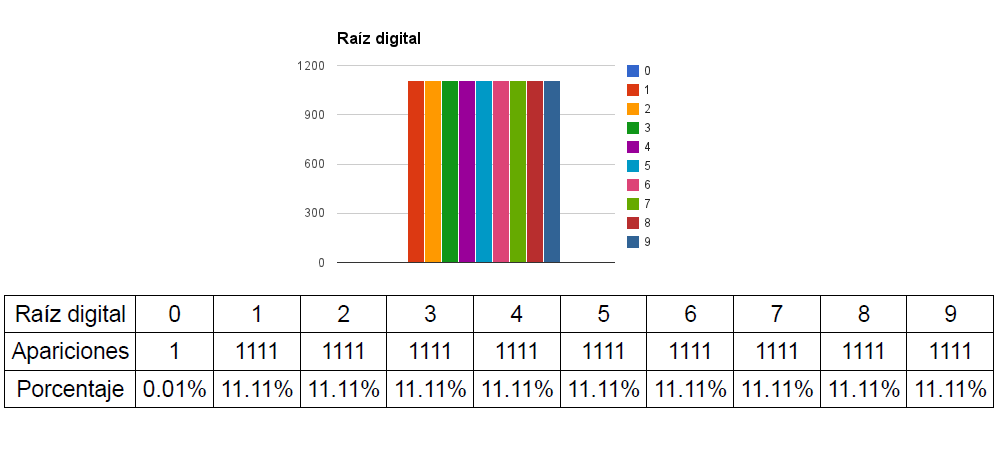
Ahora le pedimos al ordenador que recorra los números del (0000) al (9999) y anote cuántos de ellos tienen raíz digital (0), cuántos raíz digital (1),… y así hasta raíz digital (9). El resultado es éste:
(Observa que la raíz digital (0) sólo puede aparecer una vez, para la matrícula (0000)).
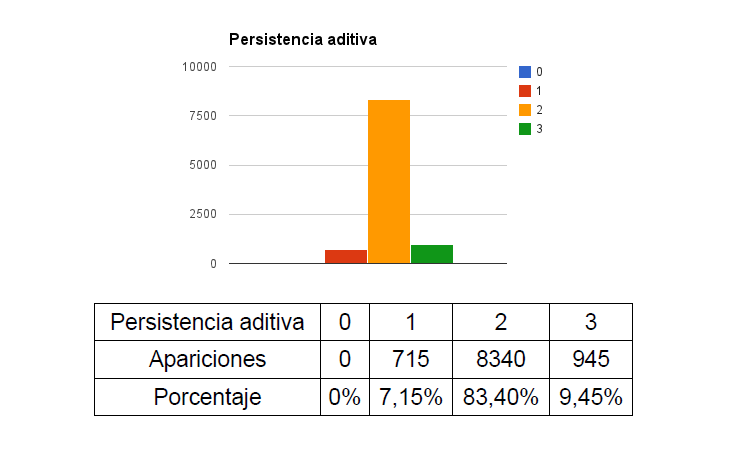
Ya que estamos, para cada número también le pedimos al ordenador que calcule la persistencia aditiva, y que cuente cuántas veces es (0), cuántas veces es (1), etc… El resultado es éste:
(Observa que estamos considerando que para las matrículas desde (0000) hasta (0009) sí hay que hacer una suma. El caso en el que no habría que hacerla sería cuando tuviéramos una matrícula con sólo un dígito).
¿Y cómo interpretamos estos resultados? Ya sabes que al tirar una moneda al aire hay una probabilidad del 50% de que salga «cara» y una probabilidad del 50% de que salga «cruz» (los 2 casos son igual de probables). Por eso, podríamos esperar que si tiras una moneda al aire 2 veces obtengas 1 vez «cara» y 1 vez «cruz». Pero eso es un comportamiento esperado; como sabes (puedes hacer la prueba) no siempre se obtiene este resultado. Lo que sí es cierto es que:
El resultado obtenido se acercará tanto más al esperado cuanto mayor sea el número de veces que hagas la prueba. (Ley de los grandes números).
De manera análoga, al preguntar a los lectores una matrícula hay una probabilidad del 0.01% de que salga (0000), una probabilidad del 0.01% de que salga (0001), una probabilidad del 0.01% de que salga (0002)… y así para cada uno de los 10.000 números (todos los casos son igual de probables).
Por eso, si hubiéramos tenido 10.000 respuestas podríamos esperar que cada una de ellas fuera uno de los números entre el (0000) y el (9999)… pero, igual que sucede al tirar la moneda al aire, esto es un comportamiento esperado y seguramente no sería lo que sucediera.
Lo que sí es cierto, por la Ley de los grandes números, es que cuantas más respuestas recopiláramos más nos acercaríamos a este comportamiento esperado y, con ello, a los porcentajes de estas últimas tablas.
Para saber más:
Si te interesa puedes descargar la gráfica de las raíces digitales y/o la gráfica de las persistencias aditivas para los números entre (0000) y (9999) (es probable que tengas que hacer zoom para verlas bien). Tanto estas gráficas como los recuentos anteriores están hechos con Sage, un software libre y de código abierto. Como puedes comprobar, las raíces digitales siguen un patrón muy particular. Hay una explicación sencilla para ello, pero la dejaremos para otro momento 🙂


Deja una respuesta