Hubo un tiempo, cuando no existían los DVD ni las tabletas, en que nuestros padres tenían que inventarse juegos para entretenernos durante los viajes en coche. Muchos de ellos servían, de paso, para aprender y agilizar la mente.
Hoy te propongo un juego que comienza sumando las cifras de tu matrícula. Si quieres ver cómo sigue, ven a jugar con nosotros.
Corren los años 80, terminan las vacaciones y un Ford Fiesta de la época viaja de vuelta a Santander. A la altura de Torrelavega, a menos de 30 kilómetros, aparece el atasco de siempre. La ciudad tiene uno de los habituales cruces de dos carreteras importantes y puede pasar un buen rato hasta dejar atrás el atasco, a pesar de los esfuerzos del guardia de tráfico y su característico espectáculo.
En el coche un niño se impacienta y sus padres, que ya han agotado la colección de casetes, buscan otra manera de entretenerle. Con la vista perdida en la matrícula del coche de delante, se les ocurre proponer al niño que sume las cifras de la matrícula. Y así, entre matrículas y sumas, pasan el atasco.
Unos cuantos años más tarde, aquel niño te propone un juego parecido:
Suma todas las cifras de tu matrícula. Si el resultado tiene más de una cifra, súmalas todas de nuevo. Sigue así hasta que obtengas un resultado con una sola cifra.
Por ejemplo, si el número de tu matrícula es (8483) tendrás que hacer:
[8483 stackrel{mbox{Suma}}{longrightarrow} 23 stackrel{mbox{Suma}}{longrightarrow} 5]
Al número de una sola cifra obtenido así se le llama raíz digital del número original. Así, el número (8483) tiene raíz digital (5).
También es interesante ver cuántos pasos hemos dado hasta terminar el juego, es decir, cuántas veces hemos tenido que sumar todas las cifras; en este caso (2) veces. Ahora imagina que tu matrícula es (5978). Si calculamos su raíz digital tenemos:
[5978 stackrel{mbox{Suma}}{longrightarrow} 29 stackrel{mbox{Suma}}{longrightarrow} 11 stackrel{mbox{Suma}}{longrightarrow} 2]
Y ahora hemos tenido que sumar todas las cifras (3) veces hasta llegar a tener una sola. A este número de veces que hay que sumar todas las cifras hasta terminar el juego se le llama persistencia aditiva.
¿Te animas a calcular la raíz digital y la persistencia aditiva de tu matrícula? Si te animas, puedes introducir los resultados (la matrícula no hace falta) en este cuestionario anónimo y os iré contando cuántas veces aparece cada resultado. ¡Espero tu participación! 🙂
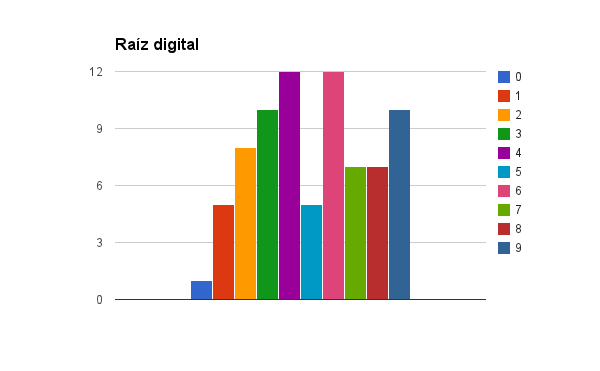
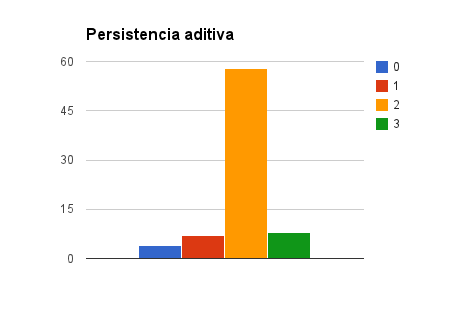
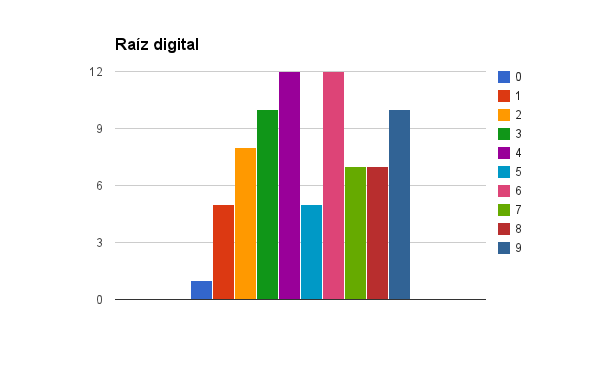
Hemos llegado a 77 matrículas así que, en honor al anfitrión, aquí están los gráficos para la raíz digital y la persistencia aditiva:
Para saber más:
La raíz digital es un número entre (0) y (9), porque es un número de una sola cifra.
La persistencia aditiva en principio puede tomar cualquier valor. Puede ser igual a (0), si tu matrícula tiene un solo dígito (entonces no te hace falta hacer ninguna suma). Puede ser igual a (1), por ejemplo para la matrícula (0010). También hemos visto ejemplos con persistencia aditiva igual a (2) e igual a (3). Pero, aunque puede haber una matrícula con persistencia aditiva igual a (4), es poco probable que la veas porque el menor número con esa persistencia aditiva es el (19999999999999999999999), es decir, un (1) seguido de veintidós (9)s, como puedes comprobar en este enlace.
Puedes seguirnos en Twitter, Facebook y Google +.
P.D.: Esta entrada está dedicada a todos los padres que se esfuerzan por sus hijos y, en especial, a los míos.
Raiz digital:4
Persistencia aditiva: 2
__________
Raiz digital: 8
Persistencia aditiva: 1
Raiz digital: 9
Persistencia aditiva: 1
Saludos.
Raiz digital: 2
Persistencia aditiva: 2
A mi me interesa responder a la siguientes preguntas
Cuantos números cumplen cada posible par (raiz digital, persistencia aditiva) para números naturales de cuatro dígitos? Ejemplo,
(0,1)-> 1 (0000)
(1,1)-> 4 (0001,0010,0100,1000)
…
¿Hay combinaciones ilegales para números de cuatro cifras?
Muchas gracias. Lo pongo en el mismo sitio de «pero lo que más le gusta es que estemos contentos».
janderfield: Hay muchas preguntas interesantes y has hecho un par de ellas. ¡Gracias! 🙂
La parte de cuántos números cumplen cada raíz digital es fácil; basta pensar en cómo va cambiando la raíz digital al aumentar el número en una unidad.
La parte de cuántos números cumplen cada persistencia aditiva es un poco menos fácil, pero tampoco complicada; la lista en este enlace da una pista.
Después habría que juntar ambas cosas.
Estaría bien resolverlo aquí entre todos. ¿Alguien se anima?
La pregunta sobre las combinaciones ilegales es más fácil de contestar; está claro que la (0,2) es ilegal, lo mismo que la (0,n) para cualquier n a partir del 2. ¿A alguien se le ocurre alguna otra?
Yo lo que hacía era calcular que cifre había que sumar a una matrícula para que fuera capicúa, por ejemplo a 1344 hay que sumarle 97 para que se convierta en 1441, y veri se esa cifra era mayor o menor de la matrícula del coche de mis padres. Sé que es algo más complicado, pero gané mucha agilidad en cálculo mental, 😉
Raiz digital: 9
Persistencia aditiva: 1
Themis: hay unas cuantas variantes, sí. Otra es intentar conseguir la última cifra haciendo operaciones con las anteriores. También multiplicar las cifras, pero de eso hablaré otro día…
Raíz digital: 4
Persistencia aditiva: 2
Raíz digital: 6
Persistencia aditiva: 2
Raíz digital: 3
Persistencia aditiva: 2
Gracias a todos. No sé si habéis introducido ya vuestros resultados en el cuestionario online o no. Si podéis, intentad ponerlo allí, aunque por supuesto se agradecen mucho los comentarios. 🙂
Gracias a todos. No sé si habéis introducido ya vuestros resultados en el cuestionario online o no. Si podéis, intentad ponerlo allí, aunque por supuesto se agradecen mucho los comentarios. 🙂
Raíz digital: 0
Persistencia aditiva: 2
Saludos,
@DazAriadna
Vaya, perdona por poner la respuesta como comentario, ya la he añadido al cuestionario 😉
@DazAriadna
Sin problemas, Patricia. Aquí estamos para pasarlo bien 🙂
Ayer hicimos 600Km con dos niños de 6 y 2 años. No tenemos DVDs (seguimos resistiéndonos). Vimos la carretera nueva de Despeñaperros y vimos por dónde iba la antigua. Contamos molinos en La Mancha. Encontramos el punto medio entre Jaén y Madrid mirando cuánto falta según los carteles y cuánto marca el cuentakilómetros parcial. Contamos camiones, coches amarillos y señales con forma de triángulo. Jugamos al veo-veo. Contamos cuántos zapatos, ojos, dedos, uñas y ombligos había en el coche… En el próximo viaje, sumaremos matrículas. ¡Gran entrada David! Gracias por la parte que nos toca, tanto por el homenaje, como por la idea 🙂
Raiz digital:2
Persistencia aditiva: 2
———————–
Raiz digital:9
Persistencia aditiva: 3
Pues con 77 matrículas todavía es poca muestra, pero si tomamos los números del 0000 al 9999 del 1 al 9 el histograma creo que daría los mismos valores y el 0 solo tendría una ocurrencia
Ya está disponible la «solución» al juego de las matrículas. @18 El zombi de Shrödinger acertó con la raíz digital 🙂