Llevas varios días volviendo tarde del trabajo y cenando un triste sándwich de jamón y queso. Pero hoy has llegado pronto y para darte una alegría preparas una tortilla de patatas con pimientos. Aunque el resultado parece más bien un revuelto, con una forma irregular, tu amigo el matemático te explica que siempre lo podréis repartir de manera que ambas mitades tengan la misma cantidad de cada uno de los ingredientes. Y con un solo corte recto, sin hacer cosas raras. Desde ahora puede que en ocasiones veas matemáticas en tus comidas.

Pasa, pasa, ya ves qué desastre me ha salido. No sé si llamarlo tortilla o revuelto, pero espero que esté bueno. Cuando vas a cortar tu creación te das cuenta de que tienes un problema. Si fuera una tortilla bien hecha no sería difícil cortarla en dos mitades más o menos iguales, pero con esta forma tan irregular que tiene…

 

¿Por qué no la cortas tú, que para eso eres matemático? propones aliviado. Al instante sabes que la sonrisa de tu amigo presagia una de sus explicaciones.

Así que quieres ponérmelo difícil… pues te voy a sorprender. No sólo es posible cortarlo de forma que los dos comamos la misma cantidad de revuelto. Se puede hacer de una manera más equitativa todavía, de forma que:

• Tu mitad tiene el mismo volumen de huevo que la mía,
• tu mitad tiene el mismo volumen de patatas que la mía, y
• tu mitad tiene el mismo volumen de pimientos que la mía.

O sea, de manera que los dos comamos la misma cantidad de cada ingrediente. Y además con un único corte recto, nada de andar haciendo cosas raras. ¿Qué te parece?

Deja que lo piense… ¿repartir por igual cada uno de los ingredientes en ambas mitades? ¿por muy revueltos que estén? Me parece increíble.

Pues créetelo. Hay un resultado matemático que, aplicado a nuestro caso, dice que

Si en tu comida hay tres ingredientes distinguibles y con volumen, entonces es posible separarla en dos mitades que tienen exactamente el mismo volumen de cada uno de los ingredientes, usando un único corte recto.

Este resultado se conoce como el Teorema del sándwich de jamón, aunque ese nombre quizá no sea el más afortunado. En un sándwich todos los ingredientes tienen más o menos la misma forma y son más o menos planos

pero este resultado sólo necesita que haya tres ingredientes, que se puedan distinguir y que todos ellos tengan volumen.

No hace falta que tu plato tenga una forma especial, ni que los ingredientes estén colocados de ninguna manera concreta. Da igual que tengas una tortilla o un revuelto. Da igual que tengas una tarta tres chocolates, rectangular y con tres capas bien diferenciadas

o un helado con fresas y galletas, más o menos arremolinados

Siempre podrás dividir de esta manera tan equitativa, con el mismo volumen de cada ingrediente en ambos lados, usando un único corte recto.

¡Fascinante! ¿Y qué pasa si tengo más de tres ingredientes? preguntas con curiosidad.

Entonces el resultado ya no es cierto, pero siempre puedes agrupar los ingredientes en tres categorías. Por ejemplo, si tienes una paella mixta podrías agrupar los ingredientes en «arroz», «carne» y «pescado». El teorema te garantiza que existe un corte que deja en ambas mitades el mismo volumen de arroz, de carne y de pescado (aunque puede que tú tengas más calamar y yo más gamba).

¿Y si tengo menos de tres ingredientes? En este punto el teorema ha conseguido atrapar tu curiosidad.

Entonces sí es cierto; siempre puedes separar un ingrediente en dos categorías, aunque sean artificiales. Si hubieras hecho una tortilla sólo de patata, podrías dividir la patata en dos categorías, por ejemplo «patata cortada al principio» y «patata cortada al final». El teorema garantizaría un corte en que ambas mitades tendrían el mismo volumen de huevo, el mismo volumen de patata del principio y de patata del final. Así, en total ambas tendrían el mismo volumen de patata.

¿Y si le paso la batidora al huevo con la patata? sigues interesándote.

Entonces ya no podrías usar el teorema, porque necesita que los tres ingredientes se puedan diferenciar. Sí pueden estar en varios trozos, como los ingredientes de tu revuelto, pero tienen que poderse distinguir.

Muy interesante, pero ya va siendo hora de que cortes mi tortilla antes de que se enfríe, ¿no?

Esto… verás: El teorema dice que se puede hacer, pero no dice cómo hacerlo. No hay un método para encontrar ese corte.

¡Matemáticos! ¿Y cómo es posible saber que se puede hacer si no sabéis cómo hacerlo?

Más o menos como tú sabes que, si esta mañana el termómetro estaba bajo cero y ahora está sobre cero, en algún momento ha estado en el cero… aunque no sepas cuándo.

Entiendo. Pues nada, dame el cuchillo que ya corto yo. ¡¡Pero no te garantizo hacerlo de manera tan equitativa!! 😀

Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.

Algunos ejemplos más:

El teorema es cierto en dimensión (d) con (d) ingredientes:

Dados (d) objetos con (d)-volumen en un espacio (d)-dimensional, es posible dividir cada uno de esos objetos en dos partes con el mismo volumen, usando un único hiperplano.

Por ejemplo, en dimensión 1 para cualquier cuerda existe un punto (hiperplano, con dimensión 0) que la divide en dos mitades de la misma longitud.

 

En dimensión 2, para cualquier hoja de periódico existe una línea recta (hiperplano, con dimensión 1) que la separa en dos mitades que tienen el mismo área de blanco y el mismo área de negro.

Fíjate en que para esto hace falta que se pueda medir el área en negro de las letras, o sea, que no sean demasiado delgaditas. También hace falta que sólo haya blanco y negro, aunque si hay tonos de grises (o incluso colores) puedes usar el truco de dividirlos en dos categorías (por ejemplo «blanco» y «otros colores»).

Puedes tratar de imaginar en qué otros ejemplos aplicar este teorema y contárnoslo en los comentarios. Pueden ser ejemplos de comida, como un pudin de puerros y gambas o un pan de pasas y nueces, o pueden ser otro tipo de ejemplos: En un partido de fútbol, donde tienes dos equipos y un grupo arbitral, el teorema te asegura que en cualquier instante ¡¡existe un plano que deja en cada mitad el mismo volumen de árbitros, de jugadores de un equipo y de jugadores del otro!!

Para saber más:

El resultado del que hablamos puede demostrarse usando el Teorema de Borsuk-Ulam. Si quieres informarte un poco más, tienes una idea de la demostración en Mathworld, en inglés. También en inglés, te recomiendo esta entrada de Terence Tao. Si prefieres leer algo en español, puedes hacerlo en esta entrada de Pablo Soberón. El propio Pablo ha demostrado recientemente  (arXiv)» href=»http://arxiv.org/abs/1010.6191″>una generalización de este teorema, repartiendo equitativamente más de una medida (por ejemplo el volumen y también la superficie) en (k) trozos (no sólo en 2 mitades).

Si te quedas con ganas de más, puedes leer la entrada «Researchers solve ham sandwich mystery» en The Guardian, escrita por uno de los organizadores de los premios Ig Nobel.

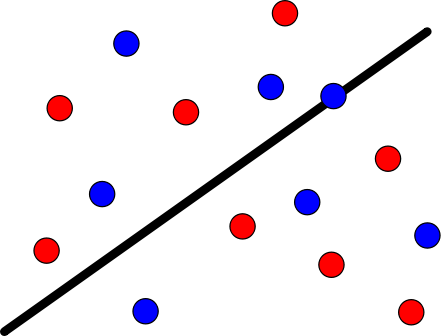
El teorema también tiene su versión discreta, en la que tenemos puntos de (d) colores en el espacio (d)-dimensional y queremos separarlos con un hiperplano, dejando a cada lado el mismo número de puntos de cada uno de los colores.

Sobre este tipo de problemas de cómo dividir equitativamente puntos de dos colores en el plano, quizá te interese este artículo, del que soy coautor.

Conviene no confundir este resultado con la Regla del Sándwich para el cálculo de límites, que es otro motivo para que el nombre del sándwich de jamón no sea del todo afortunado.

Y para terminar, una curiosidad. Resulta que en Pamplona hay un bar llamado El teorema del sandwich. La próxima vez que vaya por aquellas tierras intentaré pasar y preguntarles el porqué del nombre. Si a ti te queda más cerca cuéntanoslo, por favor 🙂

Nota 1: Quiero agradecer a Espe Saavedra su amabilidad dándome permiso para usar la imagen de su receta de revuelto de patata y pimientos. No dejes de visitar su entrada si quieres preparar uno, o su blog si quieres curiosear otras recetas.

Nota 2: Esta entrada participa en la edición 4.123105 del Carnaval de Matemáticas, cuyo anfitrión es este humilde blog.

Nota 3: Esta entrada ha llegado al Olimpo en Divoblogger.

Nota 4: Esta entrada pudo votarse en Menéame.

Nota 5: Esta entrada ha llegado a portada en Divúlgame.

Otras imágenes: La imagen del sándwich de jamón está tomada de Wikimedia Commons. La imagen de los tres chocolates está tomada de juantiagues, en Flickr. La imagen del helado con fresas y galletas está tomada de Michael Lehet, en Flickr. La imagen de la paella está tomada de Gabriel García Marengo, en Flickr. La imagen de la tortilla está tomada de Wikimedia Commons. La imagen de la cuerda y la pinza está tomada de andronicusmax, en Flickr. La imagen del periódico está tomada de Javier Leiva, en Flickr. La imagen del partido de fútbol está tomada de Jon Candy, en Flickr. La imagen de los puntos rojos y azules está tomada de Wikimedia Commons.