Éste es un problema de matemáticas que se puede explicar tranquilamente a un niño de primaria. Es ideal para que vuelvas por un rato a la infancia y juegues mientras intentas resolverlo. Sólo necesitas dibujar puntos y unirlos en línea recta.
Pero incluso lo más sencillo puede acabar complicándose y si sigues leyendo descubrirás cómo este problema se resiste a los esfuerzos de matemáticos de todo el mundo… desde hace 40 años.
Como ingredientes del problema te voy a dar un número de ciudades y un plano (una hoja de papel, una servilleta, una pantalla, sirve cualquier sitio donde puedas dibujar). El primer objetivo será:
Colocar cada ciudad, dibujada como un punto, donde queramos. Después, unir cada par de ciudades mediante una carretera en línea recta (un sueño para algunos, una pesadilla para otros ;-)).
¿Estás preparado para jugar? ¿Ya tienes con qué dibujar? Pues vamos a empezar por el caso en el que tenemos sólo 2 ciudades.
Hay que dibujar dos puntos, donde quieras, y unirlos por una carretera recta. Ya lo sé, ya, es muy fácil… pero cada uno lo habrá dibujado de una forma; unos en vertical, otros en horizontal, algunos con otro ángulo. Quizá hayas puesto los puntos muy cerca, o muy lejos, o ni una cosa ni otra.
Pero, independientemente de cómo lo haya dibujado cada uno, todos tendremos esencialmente el mismo dibujo. Esta «esencia» del dibujo es nuestro mapa de carreteras, que será igual para todos y que en este caso es un segmento:
¿Está claro, verdad? Pues ahora vamos con el caso de 3 ciudades. Hay que dibujar tres puntos y después unir cada par de ciudades mediante una carretera recta.
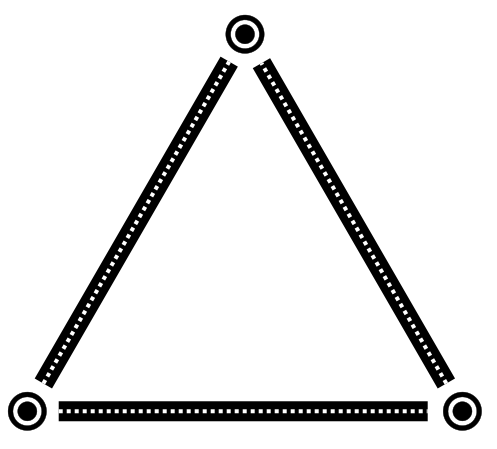
¿Lo tienes? Claro que sí. Otra vez cada uno lo habrá dibujado a su manera, pero todos tendremos un mismo mapa de carreteras, que en este caso es un triángulo:
Para 4 ciudades la cosa se pone interesante. Te dejo un rato para que dibujes. Tic, tac, tic, tac. ¿Está? ¿No has hecho trampas? Me fío de ti.
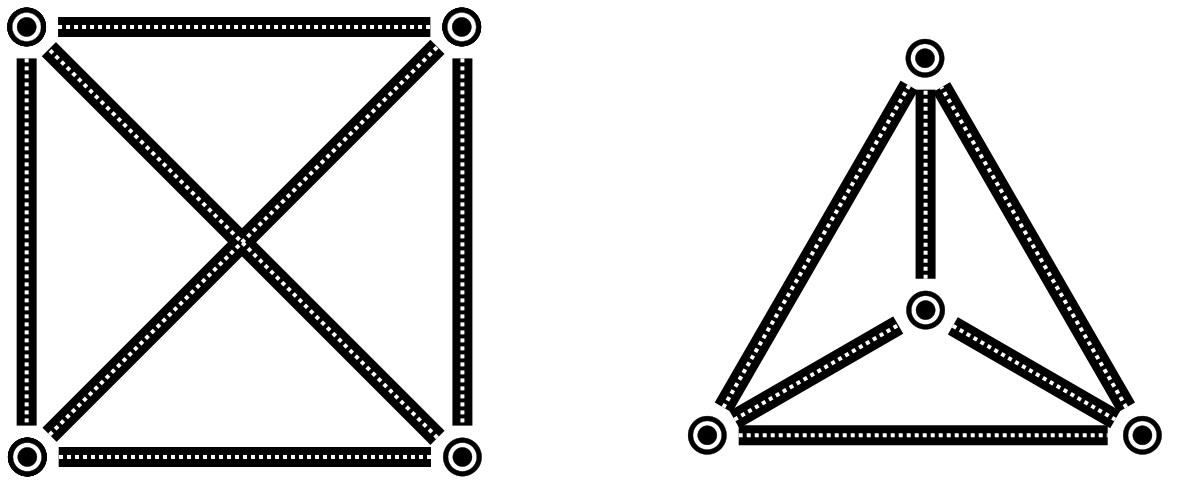
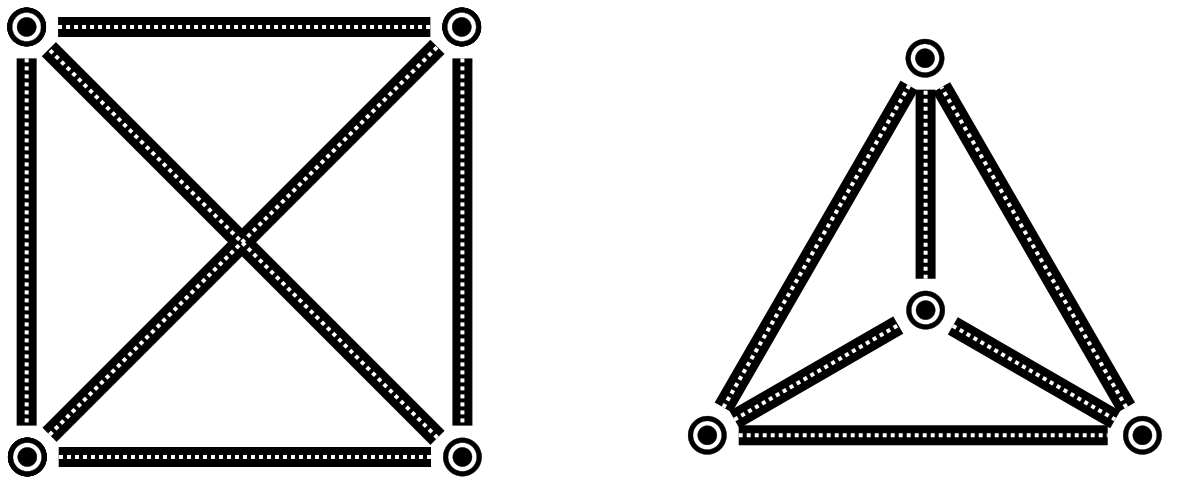
Lo interesante del caso de 4 ciudades es que hay más de un mapa de carreteras:
- Algunos habréis dibujado un cuadrilátero convexo, como el de la figura de la izquierda.
- Otros habréis dibujado un triángulo con una cuarta ciudad en su interior, como el de la figura de la derecha.
Como no habíamos puesto ninguna regla más, las dos soluciones están bien… pero en realidad una de ellas es más interesante que la otra.
El mapa de carreteras de la izquierda tiene un cruce y el de la derecha no. Como un cruce de carreteras es un peligro, vamos a intentar evitar los cruces. Así, nuestro nuevo objetivo será:
Colocar las ciudades de manera que, al unir cada par de ellas en línea recta, no aparezca ningún cruce.
¿Está claro, verdad? Pues ahora vamos a por el caso con 5 ciudades. Otro rato para que dibujes; tic, tac, tic, tac. ¿Has acabado? No me lo creo, inténtalo otro rato. Tic, tac, tic, tac. ¿Cómo? ¿Que no lo consigues? No te preocupes…
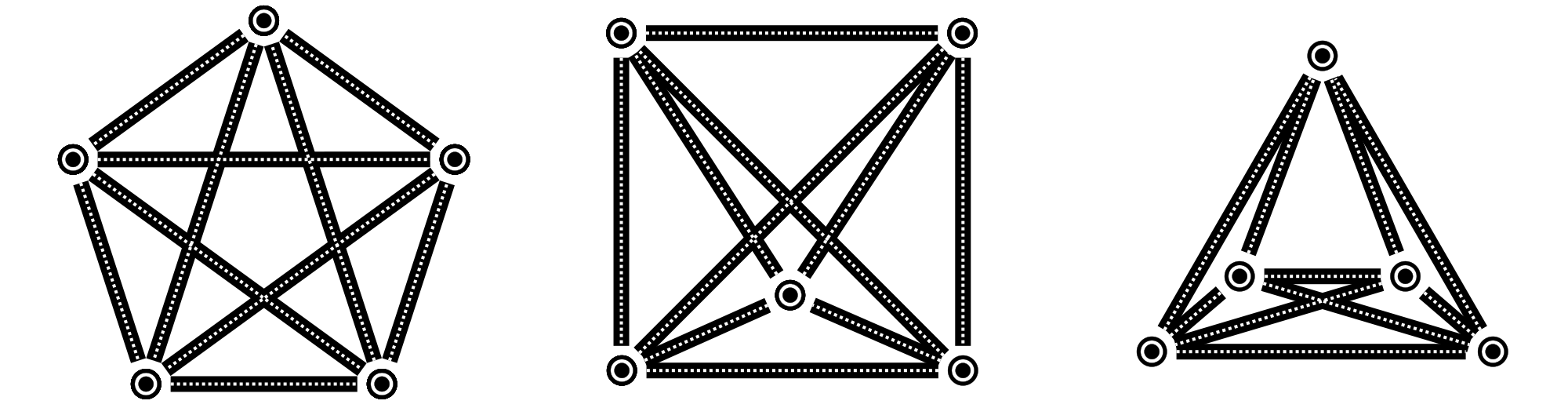
Para el caso de 5 ciudades hay tres posibles mapas de carretera:
- Un pentágono convexo (figura izquierda).
- Un cuadrilátero con un punto dentro (figura central).
- Un triángulo con dos ciudades en su interior (figura derecha).
¡¡Y en todos los mapas de carretera hay algún cruce!! Resulta que para 5 ciudades no se puede encontrar una solución sin cruces (si quieres, puedes leer por qué al final de la entrada).
Además, a partir de 5 ciudades (6, 7, 8, las que sean) cualquier mapa de carreteras contendrá un mapa de carreteras con 5 ciudades. Por lo de antes, éste tendrá cruces… así que a partir de 5 ciudades cualquier mapa de carreteras tendrá cruces.
Así que tendremos que cambiar otra vez de objetivo, pero te prometo que éste es el definitivo:
Colocar las ciudades de manera que, al unir cada par de ellas en línea recta, haya el menor número posible de cruces.
En el caso de 5 ciudades el mapa de carreteras que menos cruces tiene es el de la derecha, que tiene sólo uno, mientras que el del centro tiene tres y el de la izquierda tiene cinco.
¿Está claro el problema? ¿Te animas a seguir jugando? Puedes pensar un rato cómo colocar 6 ciudades de manera que al unirlas haya el menor número posible de cruces.
Imagínate que, después de unos cuantos intentos, lo mejor que tienes es un dibujo con 4 cruces. ¿Cómo puedes saber si has ganado? ¿Puede ser que otro jugador tenga mejor ojo y consiga hacerlo con sólo 3 cruces?
Una manera de saber si has conseguido el menor número de cruces es conocer todos los mapas de carretera distintos que puede haber. Para 6 ciudades hay 16 mapas de carretera distintos; si consigues dibujarlos todos, bastará con mirar cuál tiene menos cruces.
Pero, claro, no es fácil dibujar esos 16 mapas de carretera distintos, así que te voy a dar los resultados (no los dibujos :-)) desde 2 hasta 11 ciudades:
|
Ciudades |
Mapas de carretera |
Menor número de cruces |
|
2 |
1 |
0 |
|
3 |
1 |
0 |
|
4 |
2 |
0 |
|
5 |
3 |
1 |
|
6 |
16 |
3 |
|
7 |
135 |
9 |
|
8 |
3.315 |
19 |
|
9 |
158.817 |
36 |
|
10 |
14.309.547 |
62 |
|
11 |
2.334.512.907 |
102 |
¿Cuántos cruces habías conseguido tú para 6 ciudades? ¿Habías conseguido hacerlo con sólo 3 cruces?
Como ves, el juego se va complicando y para 11 ciudades el menor número de cruces es 102… que ya tiene que ser difícil de dibujar.
Y eso que tenemos la suerte de poder mirar en la tabla y no tener que dibujar todos los mapas de carretera distintos. Porque para 7 ciudades ya tendríamos que dibujar 135 mapas de carretera. Y para sólo 11 puntos hay ¡¡más de 2.000 millones de mapas de carretera distintos!!
Así que, aunque el problema es sencillo, se complica rápidamente a medida que crece el número de ciudades. Este problema se conoce como el problema del número de cruce rectilíneo del grafo completo y fue propuesto por Erdős y Guy en 1973. A día de hoy, 40 años después, sigue sin conocerse la solución para 28 ciudades… y eso que cualquier niño puede entender el problema.
Puedes seguirnos en Twitter, Facebook y Google +.
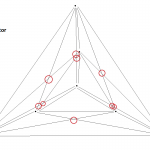
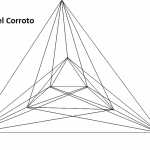
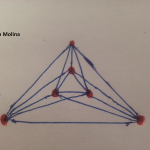
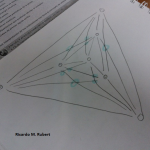
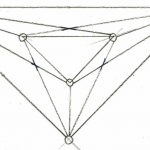
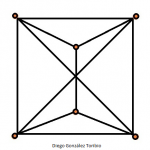
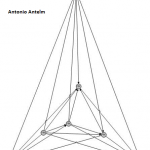
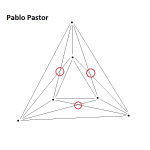
Nota 1: Si te animas a intentar conseguir el menor número de cruces para 6, 7, o incluso 8 ciudades (puedes comprobar tu resultado con la tabla), nos haría mucha ilusión que nos lo enviaras a cifrasyteclas@km77.com. Así podremos ir completando la galería, que puedes ver al final de la entrada.
Nota 2: Esta entrada participa en la edición 3.1415926535 del Carnaval de Matemáticas, cuyo blog anfitrión es La Aventura de la Ciencia.
Nota 3: Esta entrada ha llegado al Olimpo en Divoblogger.
Nota 4: Esta entrada ha llegado a portada en Menéame.
Nota 5: Esta entrada ha llegado a portada en Divúlgame.
Nota 6: Gracias a @DavidOrti por avisarme de una errata; desde 1973 hace 40 años y no 30 🙂
Para saber más:
Si te da por poner tres puntos alineados, la carretera que une las dos ciudades de los extremos pasaría por encima de la ciudad intermedia. Como eso no tiene mucho sentido, en esta entrada (y en el problema del número de cruce) se excluye esa posibilidad.
Para demostrar que el caso de 5 ciudades no se puede hacer sin cruces puedes utilizar la Fórmula de Euler; en este documento (pdf) puedes ver cómo. Este grafo para 5 ciudades se llama grafo completo (K_5) y el matemático polaco Kazimierz Kuratowski demostró que es una pieza clave para saber cuándo un grafo se puede dibujar sin cruces. Puedes leer dos entradas interesantes al respecto en este enlace o en este otro.
A cada mapa de carreteras, que en el fondo es cada manera distinta de colocar un mismo conjunto de puntos, se le llama tipo de orden. Puedes encontrar todos los tipos de orden hasta 10 puntos en este enlace. El de 11 puntos es un fichero que ocupa ¡¡96GB!!
A partir de 11 ciudades ni si quiera se sabe cuántos mapas de carretera distintos hay. Así que no se puede decidir el menor número de cruces simplemente comprobando todos los mapas. Hacen falta otras técnicas y a veces se sabe cuál es el menor número de cruces pero no se sabe cómo dibujarlo.
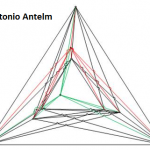
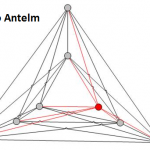
En esta página puedes ver una tabla que, hasta 100 puntos, te dice el menor número de cruces posible cuando éste se conoce, o bien el menor número de cruces que se ha conseguido, cuando no se conoce cuál es el menor posible. Como puedes comprobar, para 28 puntos hay un dibujo con 7234 cruces, pero no se sabe si hay alguno con menos cruces (si consigues uno con 7233 te harás famoso ;-)).
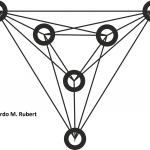
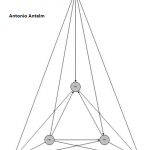
Se sabe que para conseguir el menor número de cruces la envolvente convexa debe ser triangular. Es decir, que la capa exterior debe formar un triángulo. Aunque esto se intuye fácilmente después de un par de dibujos, no se consiguió demostrar hasta 2006 en este artículo (en el que tuve el gusto de participar).
Los problemas sobre minimizar el número de cruces tienen aplicaciones, por ejemplo, en el diseño de circuitos integrados (VLSI).


Deja una respuesta