Los famosos «doce puntos» de Eurovisión esconden mucho más de lo que parece: toda una red de relaciones entre los países de Europa que sale a la luz gracias a las matemáticas.

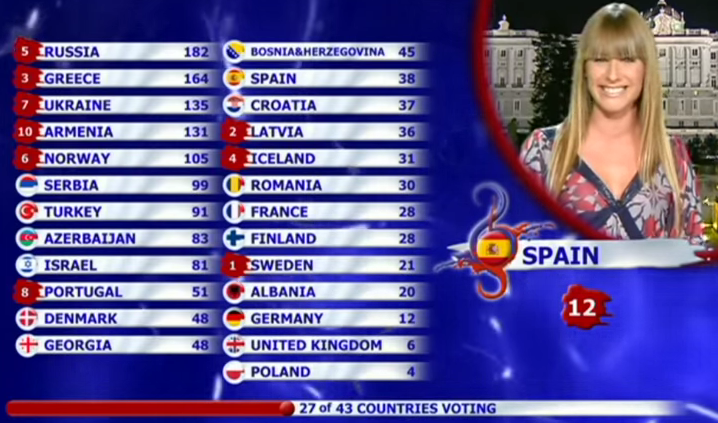
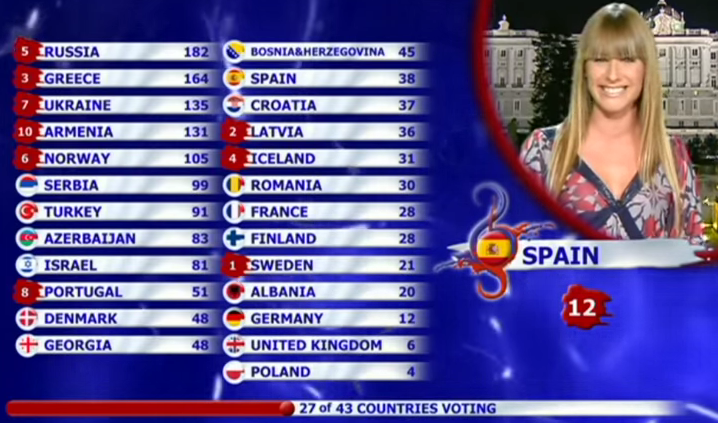
Observa con atención la siguiente imagen. ¿A qué país dará España sus doce puntos en Eurovisión? No, a Portugal no, que ya ha recibido nuestro ocho.

Si piensas que es Francia, es porque muy probablemente seas francés. Si en cambio has elegido Rumanía, es que estás al tanto de la realidad europea [1].

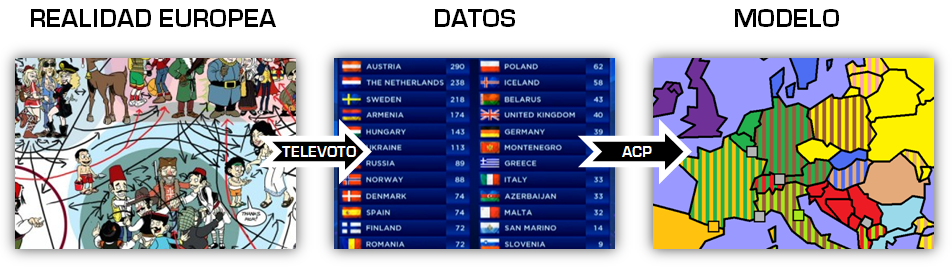
De hecho, solo con observar las votaciones de Eurovisión un año, podemos elaborar una gran red de relaciones entre los distintos países de Europa. En definitiva, todos somos testigos de cómo unos puntos, unos números, esconden vínculos entre países.

Está conversión de datos cualitativos en cuantitativos nos permite elaborar un modelo completo de las relaciones en Europa que nos resuma todas ellas en unas pocas. Para ello utilizaremos el Análisis de Componentes Principales (ACP), una técnica que reduce el número de variables de una situación inicial manteniendo buena parte de la varianza original si existen correlaciones elevadas entre sus variables [2].

El empleo del ACP en una tabla de doble entrada que recoja las votaciones medias del televoto de los últimos años nos arroja el resultado esperado: el modelo resume las 47 variables originales (países) en 11 variables latentes (patrones) explicando casi el 80% de la varianza total de los datos. Es decir, con tan solo un cuarto de las variables se sigue reflejando más de tres cuartos de la situación inicial.

El siguiente paso consiste en estudiar a fondo cuáles son estas 11 variables que componen Europa. Sin embargo, tampoco hay que irse a un problema de once dimensiones para identificar estos grupos. Si representamos las votaciones en tan solo dos dimensiones los grupos son bastante obvios, mapa y códigos en mano.

Después de un rápido vistazo habrás podido comprobar cómo los antiguos países de la élite soviética (amarillo) se emplazan a la derecha del eje de coordenadas. En la zona superior se ubican los pertenecientes a la antigua Yugoslavia (rojo). Abajo identificarás a la triada báltica (rosa). El resto es más difuso pero se ven otras relaciones como España con Portugal o el Reino Unido con Irlanda.

La primera dimensión o característica es la soviética (eje de abscisas) mientras que la segunda es la yugoslava (eje de ordenadas), dos de los grupos más evidentes cada año.

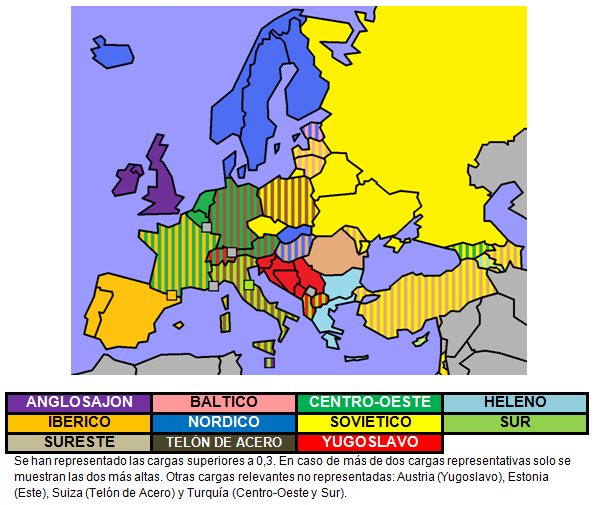
Si seguimos añadiendo dimensiones, obtendremos el siguiente mapa. La distribución es bastante compacta y atiende a diversos criterios, siendo el más relevante la demografía. Además, nos revela que en Europa rigen otras características más allá de ser ex soviético o ex yugoslavo que definen la riqueza social del viejo continente.

El modelo nos aporta también el grado en el que cada país posee cada una de las características. Con ello, algunos países presentan varias características representativas comunes, como Austria y Suiza.

Una lectura más extensa de los componentes nos revela no solo quiénes los integran, sino que también nos dicen el porqué, es decir, a donde se encaminan los votos de dichos países. Por lo general, suelen ir hacia sus propios integrantes (los famosos intercambios) pero también hay grupos que destinan sus votos a terceros países, especialmente los occidentales (como España con Rumanía).

En definitiva, pasando Eurovisión por este filtro matemático obtenemos una imagen completa de Europa y de las características que la definen. Si quieres saber más sobre esta investigación y ver qué más se esconde tras las votaciones, puedes consultar mi trabajo: “LOS SISTEMAS DE VOTACIÓN EN EUROVISIÓN: UNA RADIOGRAFÍA SOCIAL DE EUROPA”, ganador de la primera edición del concurso Utiliza matemáticas.

Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.

Nota 1: Esta entrada participa en la Edición 5.6: Paul Erdős del Carnaval de Matemáticas, cuyo anfitrión es este mismo blog.

[1] Puedes ver el desenlace aquí. Este es un claro ejemplo de desviación. Si te fijas, Rumanía venía promediando un punto por país (30 puntos / 27 votaciones) y sin embargo recibió doce de España, muy alejado del promedio.

[2] Un ejemplo del alto grado de correlación entre las variables se muestra en el siguiente gráfico, donde el promedio de votaciones dadas por Rusia, Ucrania y Bielorrusia es prácticamente idéntico.

La segunda imagen, sobre la votación de España, es una captura de este vídeo. En el esquema, la imagen de la izquierda aparece en varias fuentes (sin que haya conseguido encontrar la original), la imagen central está sacada de oikotimes aunque es una captura de Eurovisión 2014, y la imagen de la derecha es de elaboración propia. Tanto la primera imagen, como el eje de coordenadas, el mapa y el gráfico de medias son también de elaboración propia.