Aquí va un pequeño desafío:
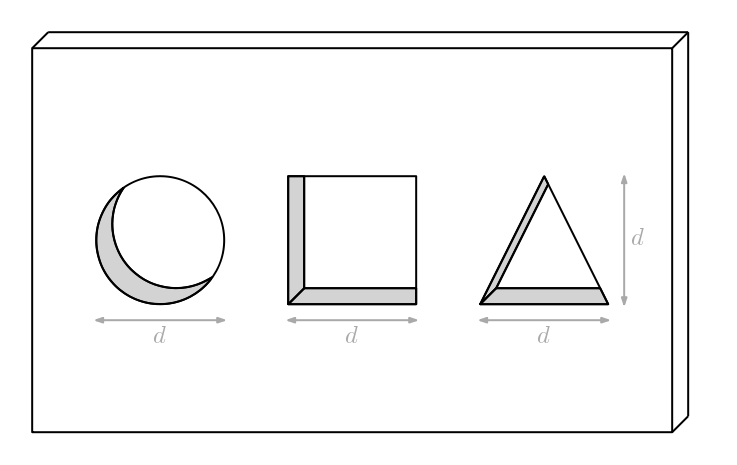
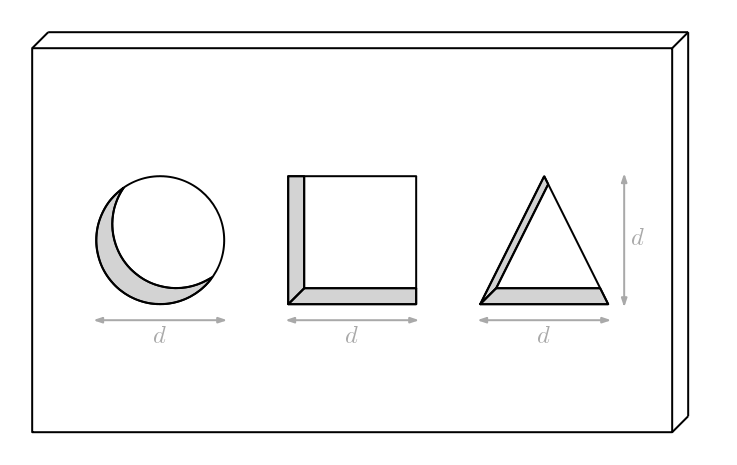
Este puzzle para bebés tiene tres agujeros: Uno circular con diámetro (d), otro cuadrado con lado también (d) y el otro triangular con base y altura también (d). ¿Podrás construir una figura 3D que pase por los tres agujeros sin dejar espacio libre alrededor?
La solución está un poco más abajo pero, como siempre, te dejo que lo pienses un rato.
.
.
.
(estás haciendo scroll)
.
.
.
.
.
.
La forma más fácil de imaginar la solución es pensar en la cabeza de un destornillador plano. Si quieres una descripción más matemática, puedes hacer lo siguiente:
- Toma un cilindro con diámetro y altura (d) y en él dibuja un diámetro en la cara superior y otro, perpendicular al de antes, en la cara inferior.
- Después corta el cilindro con un plano que contenga todo el diámetro superior y un extremo del diámetro inferior.
- Por último, corta también con un plano que contenga todo el diámetro superior y el otro extremo del diámetro inferior.
Este problema, propuesto mi compañera de departamento Arantxa Fraile a sus alumnos de la Facultad de Educación en la Universidad de Alcalá, está tomado del libro Mathematics for Elementary Teachers: A Contemporary Approach.
Me encantaría que contaras tu experiencia en los comentarios, sobre todo si te animas a proponer este problema a tus alumnos.


Deja una respuesta