Hace ¡ya tres años! di con una sorpresa al hacer el primer corte en el roscón de reyes y escribí sobre cómo de probable era. Desde entonces he incorporado a la tradición tomar medidas del roscón y las sorpresas; cualquier excusa es buena para aprender matemáticas. ¿Te animas a intentarlo?

Primer paso: Colocar un hilo o cordón sobre tu roscón, a lo largo de una curva intermedia entre el borde interior y el exterior.

Segundo paso: Medir el trozo de hilo utilizado.

Tercer paso: Comerse el roscón, recordando si nos hemos encontrado sorpresa al hacer el primer corte.

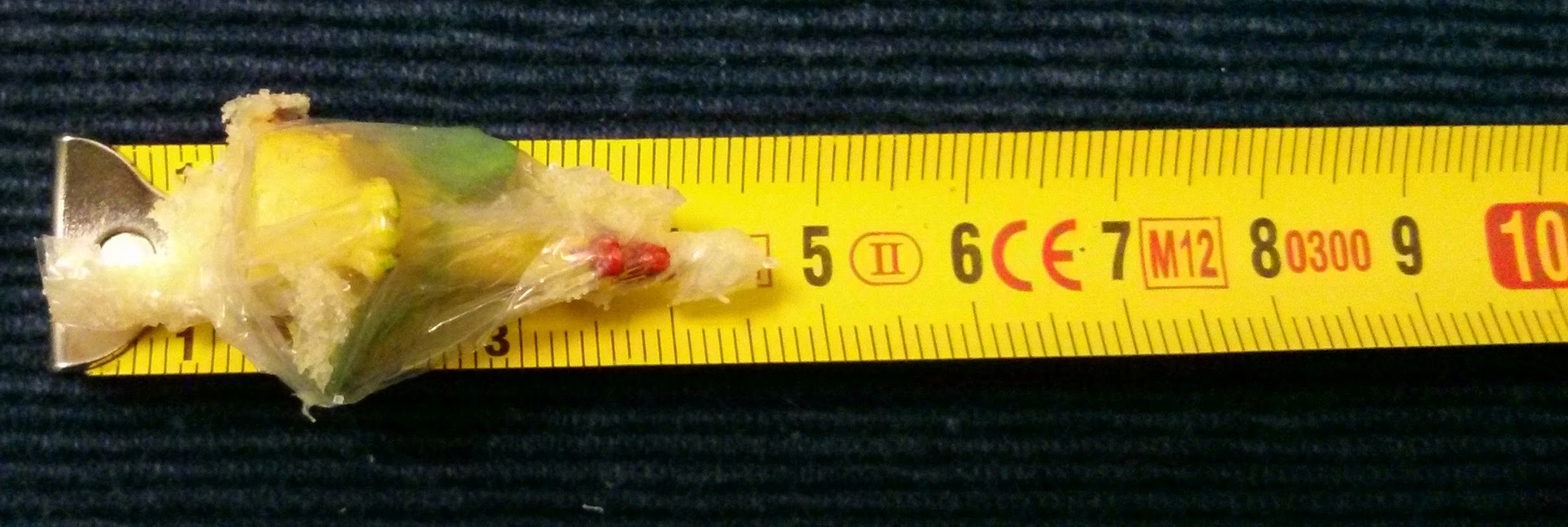
Cuarto paso: Medir las sorpresas que traía nuestro roscón.

Quinto paso: Dividir la suma de longitudes de las figuras entre la longitud del hilo utilizado. En mi caso sería 

aproximadamente, un 14% (efectivamente, no encontré la figura en el primer corte).

Aunque esto nos dará solo una estimación, es una buena manera de comprobar que estamos rodeados de matemáticas (uno de los Siete consejos para evitar que tu hijo las odie).

¡Buen provecho!

Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.

 AMPLIACIÓN:

En Twitter, Alberto S. (@alberto_et_al) sugiere incluir la probabilidad de encontrar esta figura en el primer trozo, suponiendo que éste mide 5 centímetros de arco. Como se ha tomado la molestia de enviar los cálculos, lo menos que puedo hacer es incluirlos aquí. ¡Gracias!

En caso de haber más figuras, la cosa se complicaría un poco, pero si alguien se anima y tiene tiempo será más que bienvenido.