Recién publicado un artículo, el investigador divulgador quiso salir de su despacho y contárselo a todo el mundo.

Caminó y caminó… y con el compañero viajero se encontró.

¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «Será en forma de cuento» le explicó.

 

Así acompañado, el investigador divulgador caminó y caminó… y con el conserje sonriente se encontró.

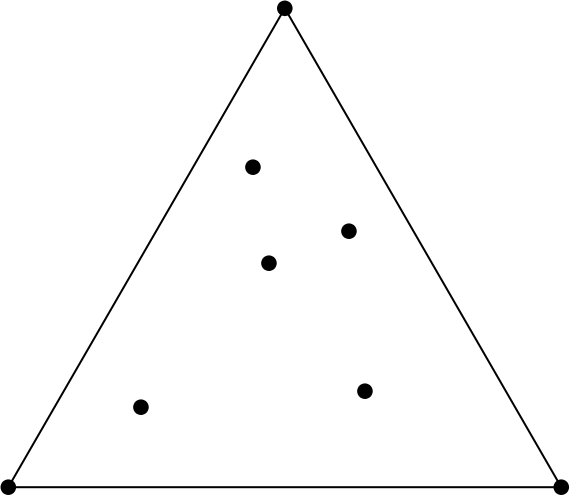
¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «Dibuja un triángulo y puntos dentro» le pidió.

Así acompañado, el investigador divulgador caminó y caminó… y a la camarera mañanera se encontró.

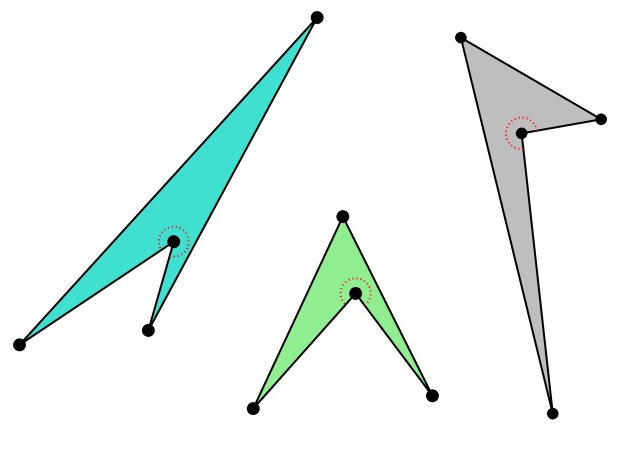
¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «Dibuja polígonos en forma de bumerán« le pidió.

Así acompañado, el investigador divulgador caminó y caminó… y con el ingeniero tuitero se encontró.

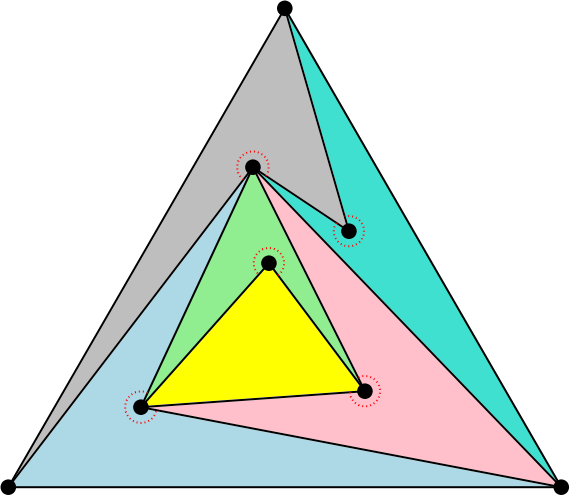
¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «Rellena el triángulo con bumeranes, dejando más de 180º libres alrededor de cada punto» le pidió.

Así acompañado, el investigador divulgador caminó y caminó… y con el administrativo efectivo se encontró.

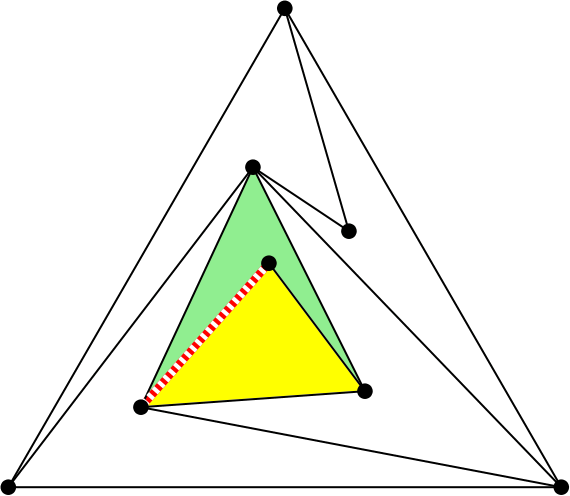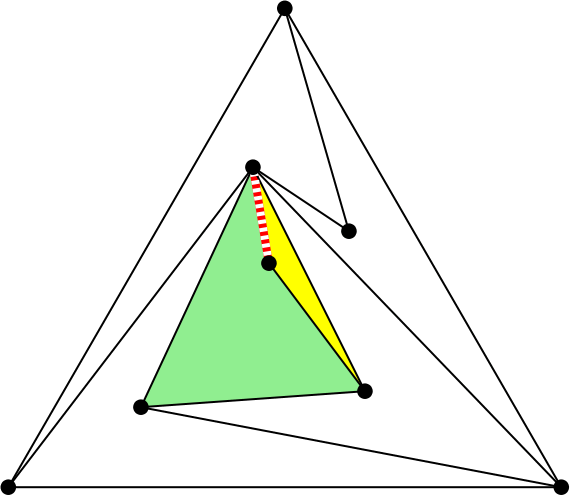
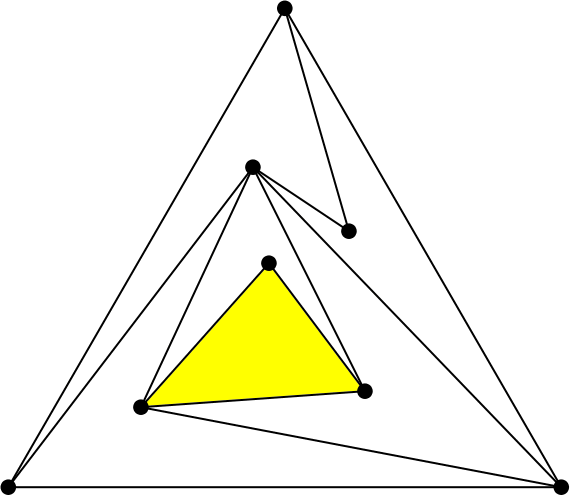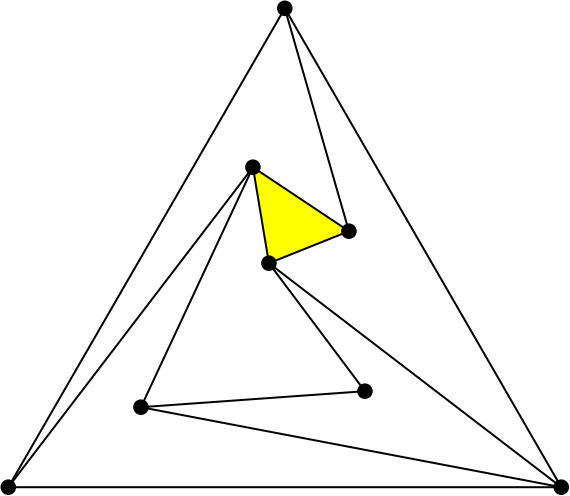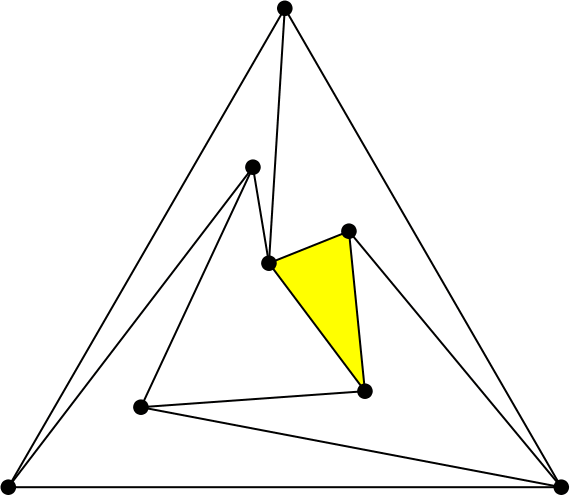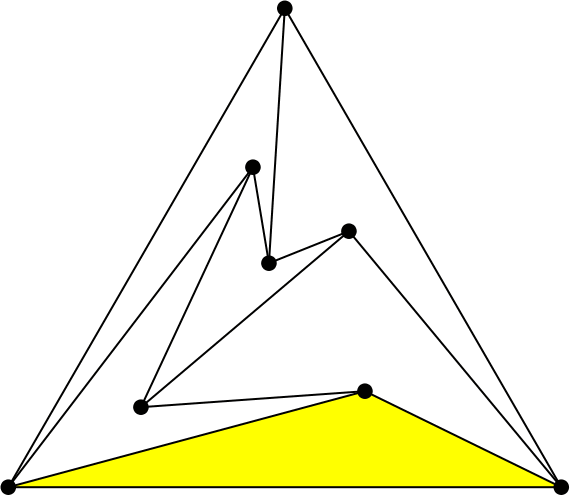
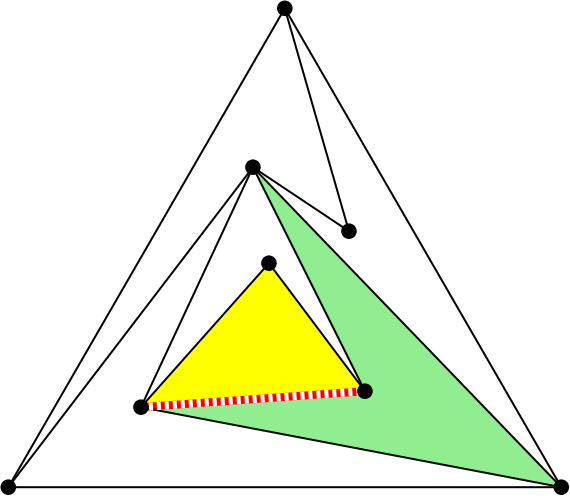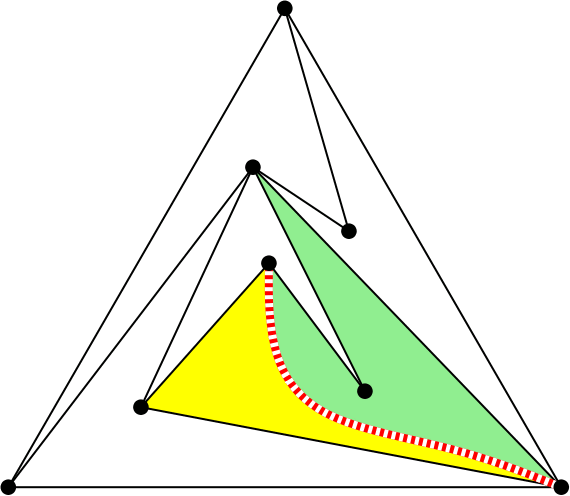
¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «Borra un segmento del triángulo y pinta otro, de forma que siga habiendo solo un triángulo» le pidió.

Así acompañado, el investigador divulgador caminó y caminó… y con el estudiante expectante se encontró.

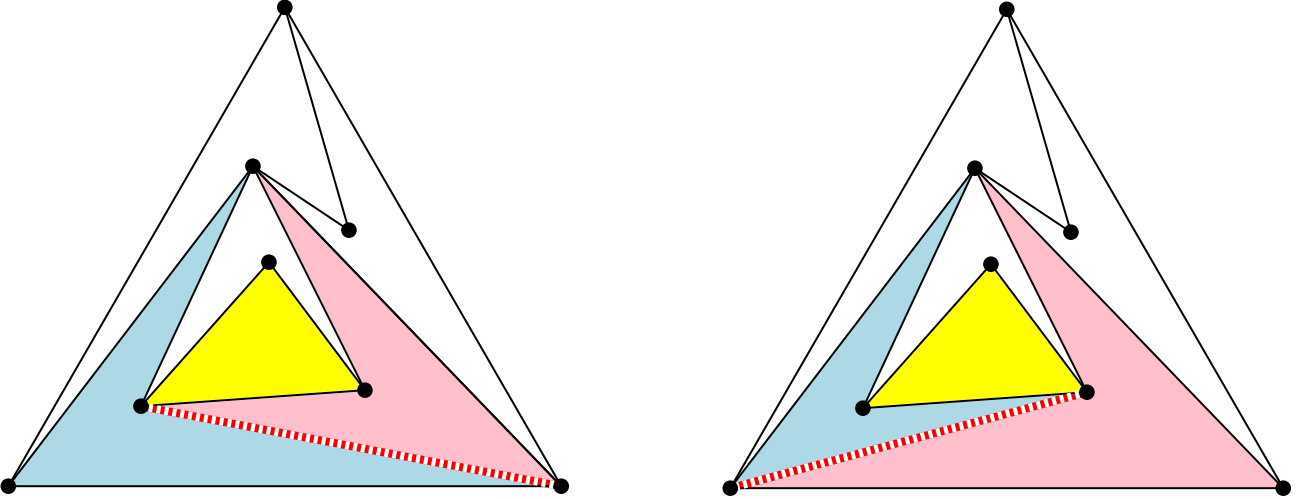
¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «Usa lo anterior para mover el triángulo de un sitio a otro» le pidió.

Así acompañado, el investigador divulgador caminó y caminó… y con la bibliotecaria visionaria se encontró.

¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «No se sabe si se puede mover el triángulo a donde quieras» le explicó.

 

Así acompañado, el investigador divulgador caminó y caminó… y con el gestor trabajador se encontró.

¿Quieres que te cuente un artículo? le preguntó. Y como no dijo que no… «En el artículo lo conseguimos usando curvas en vez de rectas» le explicó.

 

Y así, en equipo, el investigador divulgador, el compañero viajero, el conserje sonriente, la camarera mañanera, el ingeniero tuitero, el administrativo efectivo, el estudiante expectante, la bibliotecaria visionaria y el gestor trabajador siguieron su camino.

Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.

Nota 1: Esta entrada se puede votar en Menéame. ¡Gracias!

Nota 2: Esta entrada está dedicada a todos los que nos hacen el trabajo un poco más agradable y fácil. ¡Gracias!

Nota 3: Esta entrada participa en la Edición 6.X «El grafo» del Carnaval de Matemáticas, cuyo anfitrión es este mismo blog.

Para saber más:

Si haces clic en la penúltima imagen (la de los interrogantes) encontrarás una animación con una solución.

La estructura de este cuento está inspirada en El camino de Olaj. Esto de contar matemáticas como si fueran un cuento me ha recordado la viñeta «Fairy Tales» de XKCD:

Las figuras de las que se habla en la entrada, que rellenan un conjunto de puntos con bumeranes y triángulos reciben el nombre de 4-PPTs. Son pseudo-triangulaciones puntiagudas (de las que ya te hablé hace un tiempo) cuyas caras están formadas por no más de 4 segmentos.

La operación de borrar un segmento y cambiarlo por otro se denomina flip (giro es la traducción usual al español). Se usa mucho en triangulaciones, con aplicaciones en informática gráfica y modelos digitales del terreno. Puedes encontrar más información sobre los flips en la entrada Flip me to the moon que escribí para Mapping Ignorance.

Resulta que en una 4-PPT los segmentos del triángulo siempre se pueden «flipar» (girar) y por eso son los que propongo usar arriba. Pero es habitual que también otros segmentos admitan un flip.

La pregunta de si, usando flips, se puede viajar de cualquier 4-PPT a cualquier otra es uno de los problemas abiertos más interesantes en pseudo-triangulaciones. Nuestro artículo da un primer paso para resolverla, demostrando que sí se puede para 4-PPTs combinatorias. Usan curvas en vez de segmentos rectos y basta que los ángulos estén etiquetados como «grandes» o «pequeños» sin ser realmente mayores o menores de 180º.

Puedes encontrar más información en el artículo, titulado Flips in combinatorial pointed pseudo-triangulations with face degree at most four.

Imágenes:

La imagen de la madrastra dando a Blancanieves una manzana es de Pascal, en Flickr. Salvo la imagen de XKCD, el resto de imágenes son de creación propia. Todas tienen licencia Creative Commons.