Cuando uno busca aprender y ayudar a aprender, se agradece mucho recibir comentarios, sugerencias y preguntas. Hace unos días un lector enviaba esta pregunta, que es una buena excusa para pensar un rato:
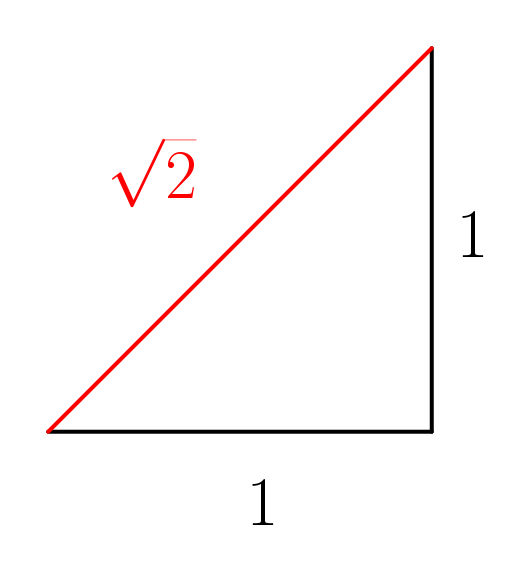
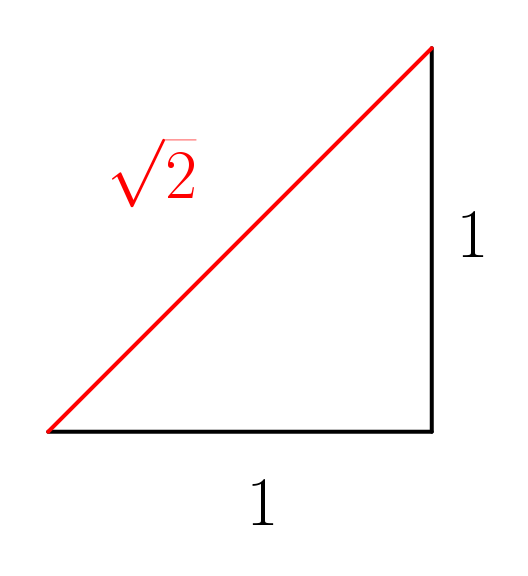
Si (sqrt{2}) es un número con infinitos decimales… ¿cómo es posible que, al definirlo como la hipotenusa de un triángulo rectángulo con catetos de tamaño (1), tenga un principio y un fin?
Al lector ya le di mi explicación, que quedó por escrito y prometo traer pronto. Pero seguro que todos podemos aprender algo si tú también nos cuentas cómo lo explicarías. ¿Te animas a hacerlo en los comentarios?


Deja una respuesta