¿Qué es más probable, que tu matrícula repita algún número o que no?

26 de octubre de 2015

En un comentario a la anterior entrada, Ismael planteaba una pregunta que había surgido en su foro:

¿Cuál es la probabilidad de que en tu matrícula se repita algún número?

La respuesta es sencilla y puede resultar curiosa. Vamos por partes, haciendo las cuentas para el caso de las matrículas actuales en España, con cuatro números, por ser el origen de la pregunta.

En lugar de calcular la probabilidad de «que se repita algún número», vamos a calcular la probabilidad de lo contrario, «que todos los números sean distintos». Ésta probabilidad, que va a ser más fácil de obtener, está dada por la fracción $\frac{\text{Casos con todos los numeros distintos}}{\text{Todos los casos}}.$

El total de casos posibles es fácil de calcular. En la parte de los números de la matrícula hay cuatro «casillas» que rellenar, y cada casilla puede tomar uno de entre los diez valores $\{0,1,2,\ldots,9\}$ . Eso hace un total de $10\cdot 10\cdot 10\cdot 10=10^4=10000$ posibilidades.

Números del 00 al 99 — Éstas son las $10\cdot 10=10^2=100$ posibilidades con dos «casillas» que rellenar.

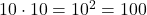Éstas son las $10\cdot 10=10^2=100$ posibilidades con dos «casillas» que rellenar.

También es fácil calcular cuántos casos con todos los números distintos hay. En la primera «casilla» puedes poner cualquier número, así que tienes 10 posibilidades. En la segunda «casilla» no puedes repetir el número anterior, así que te quedan solo 9 posibilidades. Del mismo modo, en la tercera «casilla» no puedes repetir ninguno de los dos anteriores y te quedan 8 posibilidades. Análogamente, en la última «casilla» te quedan 7 posibilidades. Así que la cantidad de casos con todos los números distintos es $10\cdot 9\cdot 8\cdot 7=5040$ .

Por tanto:

La probabilidad de que en tu matrícula no se repita ningún número es $\frac{5040}{10000}=0.504$ es decir, un 50.4%. La probabilidad de que sí se repita algún número es la complementaria, un 49.6%.

Aunque ganan las matrículas que no repiten ningún número, la probabilidad está muy repartida entre las dos opciones. ¿Cuál es tu caso?

¿En tu matrícula se repite algún número? Después de contestar, puedes leer https://t.co/4w8r0AvGWH

— Cifras y Teclas (@cifrasyteclas) October 30, 2015

Como proponía el comentario original, puedes fijarte en tu día a día a ver si encuentras (más o menos) esta proporción. También puedes hacer las cuentas para el caso de dos dígitos y comprobar tus cuentas con la imagen anterior. Cualquier excusa es buena para aprender.

Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.

Imágenes

La imagen es de Tom Magliery, en Flickr, y tiene licencia Creative Commons.

7 respuestas a «¿Qué es más probable, que tu matrícula repita algún número o que no?»

Ismael

26 de octubre de 2015

¡Gracias David! Vista tu explicación parece un problema muy sencillo. Genial.

Responder
DavidVR

26 de octubre de 2015

Curioso. ¿Podría completarlo analizando la probabilidad de que uno se repita 3 y 4 veces? ¿o dos números repetidos (dos parejas de iguales)?

Responder
Jesús

29 de octubre de 2015

Ayer leí el titulo de la entrada y antes de meterme he preferido hacer la prueba con los coches de camino al trabajo.

Y ni tan mal. De 59 matrículas 26 no tenían números repetidos, otros 26 tenían un par de ellos iguales, 5 tenían tres cifras iguales y luego 1 tenía dos pares de cifras iguales.

Para ser una muestra tan pequeña se ha acercado bastante! Como dice en el comentario anterior, ahora estaría bien saber si esta muestra se ha acercado en los casos de tres cifras, cuatro o parejas dos a dos.

En cualquier caso habría preferido no encontrarme con tanto coche…

Responder
1. David Orden
  
  30 de octubre de 2015
  
  @2 Jesús: ¡Me encanta esa actitud! :_) @1 DavidVR: Lo que me parece llamativo es que para ese caso las probabilidades estén tan igualadas. Para el resto de casos ya no me daba el tiempo 🙁 En el foro en que surgió la cuestión han hablado de esos casos, pero recomiendo pensarlo antes.
  
  Responder
Rafa Cobo

21 de noviembre de 2015

Para los que reaccionan porque hay muchos números premiados por la ONCE que tienen 2 o más cifras repetidas: ¿estoy en lo cierto si afirmo que la posibilidad de que tengamos un número de 5 cifras sin ninguna repetida es sólo del 30,24 %? (o sea 10 * 9 * 8 * 7 * 6 = 30 420; 30 240 / 100 000 = 0.3024)

Un saludo desde Noruega

Responder
kris

14 de julio de 2019

No encuentro la manera de calcular la probabilidad de que se repita por ejemplo el 333 seguido, o el 555 seguido, o el 1111 , me ayudáis? que no me apaño con las formulas?
gracias!

Responder
Wandel

2 de agosto de 2019

Le falta un numero a mi matricula de mí pasola

Responder

Deja una respuesta Cancelar la respuesta

Sobre el autor

Soy profesor del área de Matemática Aplicada en la Universidad de Alcalá. Me interesa aprender y ayudar a aprender. Me gusta conectar las matemáticas con otros campos. Cuento cosas en Twitter como @ordend. Tengo una página profesional con más información.

Sobre el blog

Este blog trata sobre matemáticas, miradas desde distintos puntos de vista. Pretende ser cooperativo, porque seguro que hay algo de lo que sabes más que otros y, aunque no lo hayas pensado nunca, tiene matemáticas detrás. Queremos pasarlo bien jugando a pensar y ayudarnos entre todos a aprender cosas. Puedes seguir a @cifrasyteclas en Twitter o visitarnos en Facebook.

Imágenes