Categoría: Geometría
-
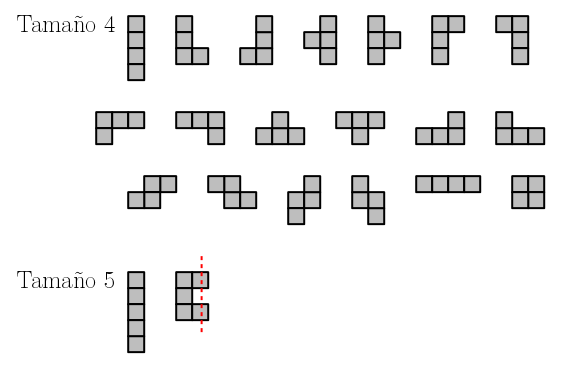
¡Feliz 2017, número de poliominós convexos por columnas!
Se acaba un año más. Un 2016 en el que no hemos podido leernos todo lo que me gustaría, entre nuevas líneas de investigación, más clases de lo esperado y algún apoyo menos de lo esperado. Pero aquí estoy, un año más, para desearos a todos un estupendo 2017 y, de paso, aprender algo nuevo.
-

El cuento de un investigador divulgador
Recién publicado un artículo, el investigador divulgador quiso salir de su despacho y contárselo a todo el mundo.
-

La probabilidad de encontrar sorpresa al primer corte en mi roscón de reyes de este año
Hace ¡ya tres años! di con una sorpresa al hacer el primer corte en el roscón de reyes y escribí sobre cómo de probable era. Desde entonces he incorporado a la tradición tomar medidas del roscón y las sorpresas; cualquier excusa es buena para aprender matemáticas. ¿Te animas a intentarlo?
-
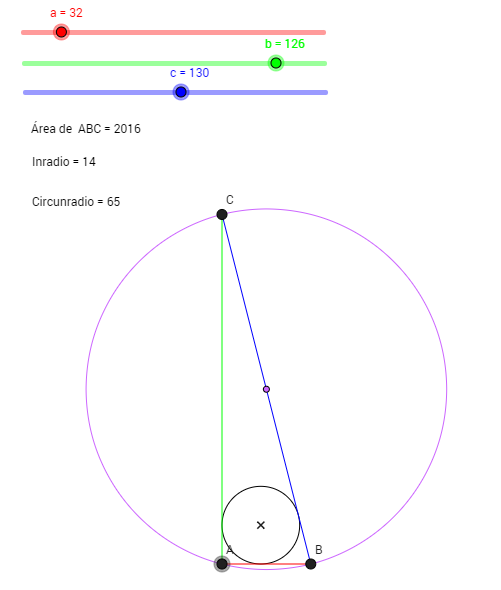
¡Feliz 2016, área de un triángulo con lados, inradio y circunradio enteros!
Apuramos las últimas horas del año 2015 y es buen momento para preguntarnos qué tiene de interesante el número 2016.
-
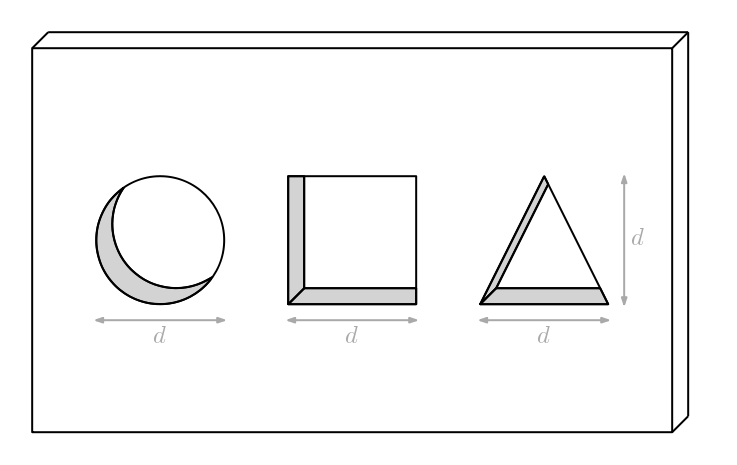
Este puzzle para bebés pone a prueba tu intuición geométrica
Aquí va un pequeño desafío: Este puzzle para bebés tiene tres agujeros: Uno circular con diámetro (d), otro cuadrado con lado también (d) y el otro triangular con base y altura también (d). ¿Podrás construir una figura 3D que pase por los tres agujeros sin dejar espacio libre alrededor?
-

¡Feliz 2015, número de triángulos rectángulos y año con blue moon!
Ya falta poco para que te empiecen a llegar mensajes, más o menos ingeniosos, felicitando el año nuevo. Si tienes amigos que no se asustan con las matemáticas, te propongo que les hables de esta curiosa propiedad del 2015. Si prefieres otra cosa, puedes hablarles de la canción Blue Moon y contarles que el próximo mes de julio tendrá dos lunas llenas.
-

Dos acertijos de Gardner para trolear y una sorprendente utilidad
Para vacilar a tu amigo le preguntas: ¿Cuántos cigarrillos iguales puedes colocar (sin doblarlos ni romperlos) de modo que cada uno toque a todos los demás? Luego le cuentas que el problema, aún sin resolver, viene de un acertijo de Martin Gardner y le propones un problema similar, con cilindros infinitos en lugar de cigarrillos. Por último, le sorprendes al contarle que este…
-
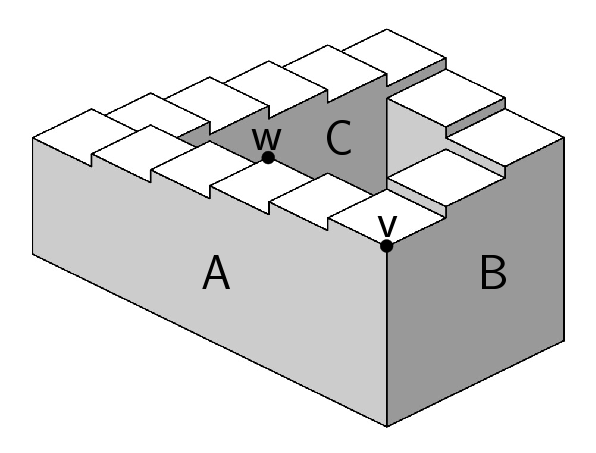
Puedes construir objetos «imposibles» usando inecuaciones
Seguro que ya has visto alguna que otra ilusión óptica. ¿Te apetece sorprenderte con objetos en 3D que parecen imposibles? ¿Y, mejor aún, entender las matemáticas que permiten construirlos? Si te animas, te llevarás un kit para construir tu propio objeto «imposible» tridimensional.
-

El problema matemático que nació en un campo de trabajo de la Segunda Guerra Mundial
La Segunda Guerra Mundial. Un campo de trabajos forzados. Vagonetas cargadas de ladrillos que, en los cruces de raíles, traquetean y pierden parte de su carga. Un matemático soldado que se pregunta si podría haber menos cruces. Ésta es la historia de un problema tan desafiante como fácil de entender, que lleva sin resolver 70 años pese…
-
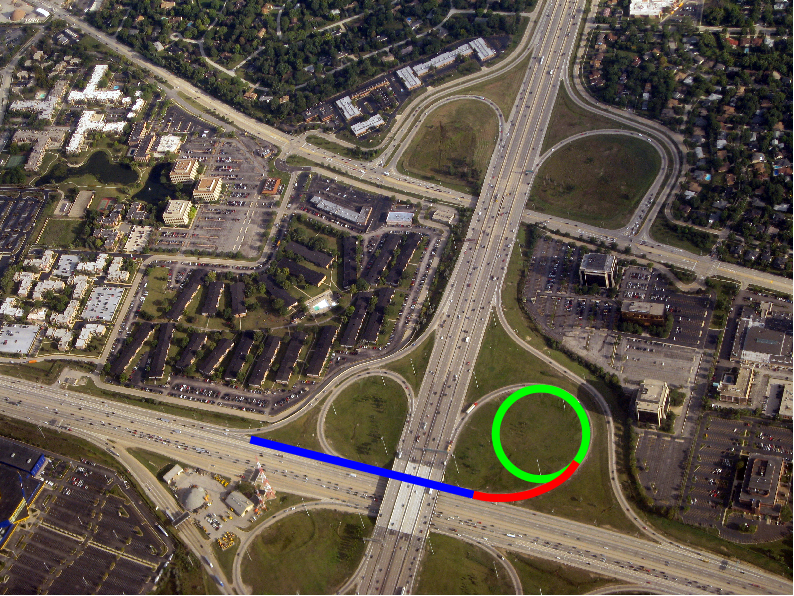
Clotoide, la curva que vela por tu seguridad en carreteras y ferrocarriles
Los primeros trazados de carreteras y vías férreas encadenaban tramos rectos con arcos de circunferencia. Pero, cuando coches y trenes alcanzaron velocidades más altas, se producía una incómoda y peligrosa sacudida al entrar en la curva. Los ingenieros comenzaron a buscar una solución, y la encontraron en las matemáticas y la física. ¿Quieres una explicación…
