La Segunda Guerra Mundial. Un campo de trabajos forzados. Vagonetas cargadas de ladrillos que, en los cruces de raíles, traquetean y pierden parte de su carga. Un matemático soldado que se pregunta si podría haber menos cruces. Ésta es la historia de un problema tan desafiante como fácil de entender, que lleva sin resolver 70 años pese a que se conjetura una solución muy sencilla.
La historia de la máquina Enigma y los trabajos de Alan Turing durante la Segunda Guerra Mundial son bastante conocidos. Pero durante la guerra surgieron otros problemas que, con menor trascendencia, también se han hecho un hueco en la historia de las matemáticas. Como el problema del número de cruce para el grafo bipartido completo que, de la mano de la conjetura de Zarankiewicz, es uno de los problemas abiertos más importantes en Teoría de Grafos.
Dejemos que sea el primer protagonista de esta historia, el matemático húngaro Paul Turán, quien te cuente cómo empezó todo:
En 1944 nuestro batallón tuvo la extrema suerte de trabajar (gracias a algunos camaradas muy ricos) en una fábrica de ladrillos cerca de Budapest.
Nuestro trabajo era sacar los ladrillos de los hornos y transportarlos, en vagonetas que circulaban sobre raíles, hasta alguno de los almacenes que estuviera vacío. Como nunca se podía estar seguro de qué almacén iba a estar disponible, cada horno estaba conectado por raíles con todos los almacenes.
Puesto que teníamos que trasladar una cantidad fija de vagonetas al día, nos interesaba terminar lo antes posible. Después de cargarlas en los hornos (bastante calientes), las vagonetas se deslizaban suavemente por los raíles sin demasiado esfuerzo; el único problema aparecía cuando se cruzaban dos raíles. Allí las vagonetas saltaban y los ladrillos se caían, suponiendo un montón de trabajo extra y una pérdida de tiempo.
Después de pasar por esta experiencia cantidad de veces, pensé por qué demonios habían construido el sistema de raíles de manera tan poco económica; minimizando el número de cruces la producción podría haber sido mucho más económica.
Paul Turán en carta a Richard Guy (1968). Traducción del autor.
Acabada la guerra, a Turán ya no le interesaba sólo aquella fábrica. Ahora quería resolver el problema matemático de cómo minimizar los cruces en cualquier fábrica con una organización similar:
- Dos tipos de edificios; hornos y almacenes.
- Cada horno unido a todos los almacenes.
- Ningún horno unido a otro horno y ningún almacén unido a otro almacén.
Los matemáticos, que somos muy de poner nombres, a esta estructura le llamamos grafo bipartido completo. Pero vamos al lío, ¿cómo puedes minimizar los cruces de tu fábrica?
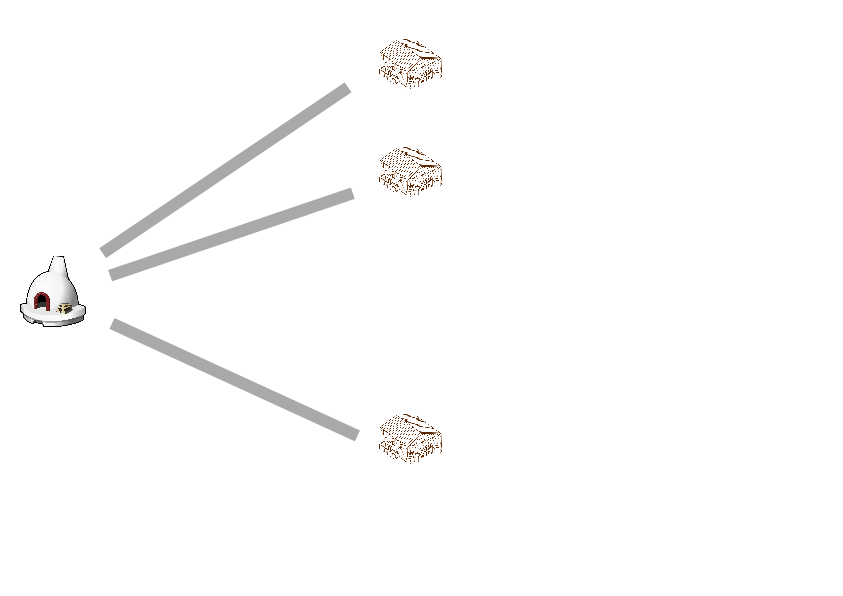
Si sólo hubiera un horno, sería muy fácil diseñar la fábrica para que no hubiera ningún cruce.
Si sólo hubiera un almacén, podrías hacer algo similar, intercambiando hornos y almacenes en el dibujo.
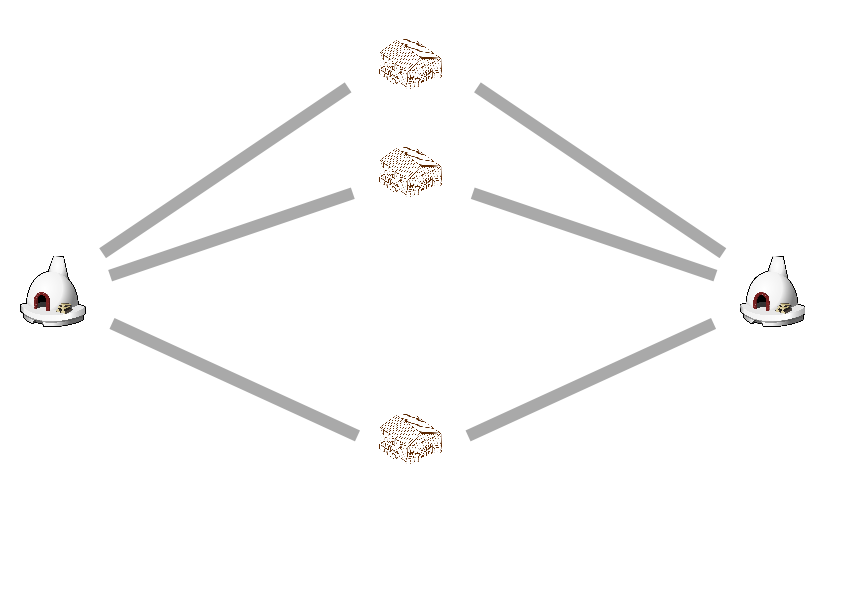
¿Y si sólo hubiera dos hornos? Enseguida se te ocurrirá cómo diseñar la fábrica para que tampoco haya cruces:
Y si sólo hubiera dos almacenes podrías hacer algo similar.
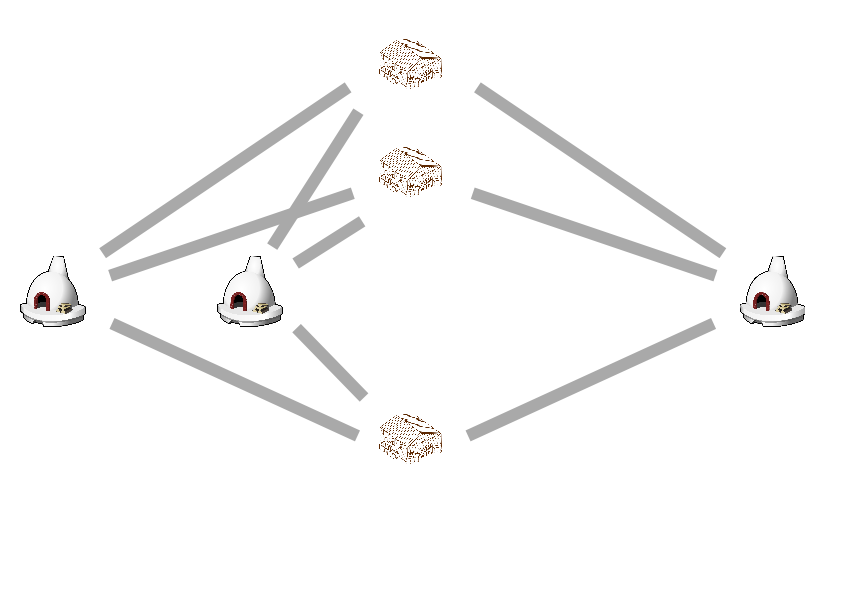
Así que lo interesante de verdad empieza cuando tienes tres hornos y tres almacenes. ¿Puedes unirlos sin ningún cruce? Tic, tac, tic, tac…
Este caso se conoce como el problema de las tres casas y los tres suministros y es un clásico de los juegos de ingenio. Tiene muchas y muy variadas versiones y, además, está relacionado con el teorema más importante del siglo XX. No te voy a enseñar todavía el dibujo por si quieres pasar un rato pensando 😉
Turán siguió aumentando el número de hornos y almacenes, pero después de pensar mucho (y dibujar un montón) algunos casos se le resistían, así que decidió plantear el problema a otros matemáticos. En 1952 lo mencionó en una conferencia en Varsovia… y aquí entra en escena el segundo protagonista de esta historia.

A esa conferencia asistió el polaco Zarankiewicz, quien poco después propuso una solución tan sencilla que parecía mentira que pudiera funcionar:
- Coloca los hornos alineados en horizontal, una mitad a la izquierda y la otra mitad a la derecha.
- Coloca los almacenes alineados en vertical, una mitad arriba y la otra mitad abajo.
- Si tu número es impar, simplemente pon en una de las «mitades» un elemento más que la otra.
Según Zarankiewicz, con eso siempre conseguirás el menor número de cruces posible. Por ejemplo, para tres casas y tres almacenes el dibujo queda así
y tiene un único cruce que (efectivamente) es lo mejor que se puede conseguir.
Además de ser un diseño muy sencillo, la propuesta de Zarankiewicz tenía una ventaja; aunque nadie lo había pedido, ¡¡sólo usa raíles en línea recta!!
Zarankiewicz publicó en una revista científica su solución y durante unos años se creyó que ahí había acabado todo… pero la historia del problema de la fábrica de ladrillos dio un giro inesperado en 1969, cuando el británico Richard Guy publicó un artículo haciéndose eco de diversos trabajos que mostraban un error en los argumentos de Zarankiewicz.
Lo que hasta entonces era un teorema, una afirmación demostrada, se había convertido en una conjetura, una afirmación que se supone cierta pero que no se ha podido demostrar ni refutar. Había nacido la Conjetura de Zarankiewicz:
¿Es realmente el diseño de Zarankiewicz la mejor manera de diseñar una fábrica de ladrillos, para cualquier número de hornos y almacenes? ¿O en algún caso se puede conseguir un diseño con menos cruces, aunque sea usando curvas en los raíles?
Desde entonces, investigadores de todo el mundo han intentado arrojar un poco de luz sobre este asunto. Pero, aunque el problema es sencillo de explicar, resulta ser endiabladamente escurridizo.
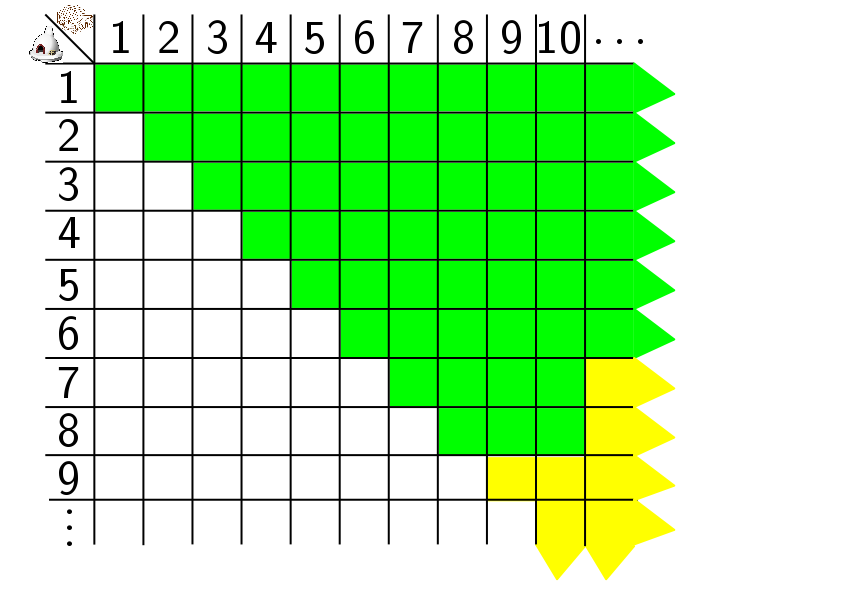
Tanto es así, que sólo se ha conseguido estar seguros de que el diseño de Zarankiewicz es el mejor para unos pocos casos, los que aparecen en verde en esta tabla:
Pero para el resto de casos sigue sin saberse si el de Zarankiewicz es realmente el diseño con menos cruces o no. ¡¡Ni siquiera se sabe cuál sería el mejor diseño para una fábrica con 9 hornos y 9 almacenes!! Si consigues uno con menos de 256 cruces (los que daría Zarankiewicz) te harás famoso. ¿A que no parece para tanto?
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Nota 1: Esta entrada ha resultado ganadora de la Edición 5.1: Rey Pastor del Carnaval de Matemáticas, cuyo anfitrión es Tito Eliatron Dixit. ¡¡Gracias!!
Nota 2: Esta entrada ha llegado a portada en Menéame. ¡Gracias!
Nota 3: Esta entrada ha llegado al Olimpo en Divoblogger. ¡Gracias!
Nota 4: Esta entrada ha llegado a Portada en Divúlgame. ¡Gracias!
Para saber más:
El relato de Paul Turán aparece en una carta a Richard Guy que éste recoge en su artículo sobre la propuesta de Zarankiewicz. Más tarde, Turán escribió un interesante texto de bienvenida para el primer número de la revista Journal of Graph Theory. Más extenso, en este texto narra además otras historias de aquellos años, incluyendo cómo obtuvo trato de favor de un oficial que era ingeniero y había trabajado como corrector en la imprenta que imprimió varios de sus trabajos matemáticos. Quizá también te interese consultar esta biografía de Paul Turán.
El número de cruces para (m) hornos y (n) almacenes con el diseño de Zarankiewicz resulta ser
[leftlfloorfrac{m}{2}rightrfloor leftlfloorfrac{m-1}{2}rightrfloor leftlfloorfrac{n}{2}rightrfloor leftlfloorfrac{n-1}{2}rightrfloor ] y a veces se le llama número de Zarankiewicz (esos simbolitos parecidos a un corchete significan «mayor número entero por debajo»). Quizá te interese leer el artículo original de Zarankiewicz.
El artículo en el que Guy desmontó la propuesta de Zarankiewicz es The decline and fall of Zarankiewicz’s theorem, del libro Proof Techniques in Graph Theory (ed. F. Harary), New York: Academic Press (1969), páginas 63–69. Aparentemente no está disponible online (si alguien lo encuentra añadiré la referencia), pero sí está a la venta en Amazon por un precio poco módico.
Si has estado dándole vueltas al caso con tres hornos y tres almacenes (o si ya lo conocías) seguro que te interesará saber que sí se puede resolver sin cruces en la banda de Möebius (nos lo contó Gaussianos) y en el toro (nos lo contaron en Trablog). Quizá también te interese leer una entrada anterior en la que hablé sobre cómo dibujar con pocos cruces otro tipo de estructura.
Los últimos resultados en la tabla de casos de la conjetura de Zarankiewicz datan de 1993 y fueron obtenidos por Woodall con la ayuda de cálculos por ordenador; puedes consultar el artículo si te interesa. Desde entonces no se ha conseguido resolver ningún otro caso de la tabla. Si quieres hacerte famoso resolviendo el siguiente caso abierto, el de nueve hornos y nueve almacenes, quizá te ayude este artículo de 2002 en el que intentaron extender, sin éxito, los cálculos de Woodall.
Después de la motivación original de Turán, han aparecido otros motivos para intentar dibujar un grafo con el menor número posible de cruces. Por ejemplo, a la hora de construir microchips. Puedes leer sobre ello en este informe o (por ejemplo) en el artículo Improved Approximations of Crossings in Graph Drawings and VLSI Layout Areas, publicado en el SIAM Journal on Computing.
Por último, puedes encontrar más enlaces e información en la entrada en inglés The fascinating history of the brick factory problem que escribí para Mapping Ignorance y que llegó hasta reddit. En el mismo blog, en la entrada Progress checking Zarankiewicz’s conjecture on the brick factory problem, puedes encontrar algunos progresos recientes relacionados con este problema. Aunque no han conseguido comprobar ningún nuevo caso en la tabla, sí que han abierto un camino que podría ayudar a resolver la conjetura a medio plazo. Quién sabe, quizá tú y yo lo veamos.
Imágenes:
Cruce de vías por Pedro Rebelo, en Flickr. Horno y almacenes de openclipart. Conferencia de Paul Turán en Wikimedia Commons.




Deja una respuesta