Los primeros trazados de carreteras y vías férreas encadenaban tramos rectos con arcos de circunferencia. Pero, cuando coches y trenes alcanzaron velocidades más altas, se producía una incómoda y peligrosa sacudida al entrar en la curva. Los ingenieros comenzaron a buscar una solución, y la encontraron en las matemáticas y la física. ¿Quieres una explicación sencilla de por qué se usa la clotoide como curva de transición?
Imagina que tienes que diseñar una autovía o una vía férrea de alta velocidad. Seguro que intentarás que haya todas las rectas posibles, pero también tendrás que hacer alguna curva. Y como la más sencilla de todas es la circunferencia, lo más fácil sería ir empalmando tramos rectos con arcos de circunferencia. Algo parecido a una cinta transportadora.
Parece que así fueron los primeros trazados y, como los primeros coches y trenes no iban a mucha velocidad, todo iba como la seda. Pero la cosa cambió cuando los vehículos fueron capaces de alcanzar velocidades mayores. Al entrar en la curva, en las uniones entre tramos, se notaba una súbita sacudida. Mal asunto.
Así que los ingenieros comenzaron a estudiar qué pasaba y cómo se podía solucionar. La respuesta es fácil de entender y sólo necesitarás dos ingredientes. El primero viene de la geometría y es el radio de curvatura, un concepto bastante intuitivo.
Para una circunferencia, el radio de curvatura es simplemente el radio de la circunferencia. Para una recta puedes pensar que ésta es una circunferencia muuuuuyyyyy grande, de radio infinito. Así el radio de curvatura de una recta será infinito. ¿Fácil, verdad?
El segundo ingrediente viene de la física y es la fuerza centrífuga, cuyo significado es aún más intuitivo, aunque tiene más miga de lo que parece.
Seguro que te suena que la fuerza es «masa por aceleración» y, simplificando un poco, la fuerza centrífuga resulta ser lo siguiente (que nadie se asuste, que viene una fórmula pero está sola y es cobarde):
![]()
donde (m) es la masa, (v) es la velocidad y (r) es nuestro amigo el radio de curvatura.
- Por un lado tienes la masa y la velocidad, que en tu fórmula aparecen multiplicando. Así que cuanto más grandes sean, mayor será la fuerza centrífuga. Tiene lógica; si vas más deprisa, la fuerza centrífuga será mayor, lo mismo que si tienes mayor masa.
- Por otro lado tienes el radio de curvatura, que en tu fórmula aparece dividiendo. Así que cuanto más grande sea, menor será la fuerza centrífuga. Tiene lógica; en una recta el radio de curvatura es infinito, así que («dividiendo entre infinito») en una recta la fuerza centrífuga es cero. También sabes que, a igual velocidad, la fuerza centrífuga es menor en una curva «más abierta» (con mayor radio) que en otra «más cerrada».
¿Hasta aquí está todo claro? Genial, porque entonces vas a entender enseguida qué pasaba en las uniones entre recta y circunferencia.
En esos puntos el radio de curvatura (r) pasaba de ser infinito (si lo prefieres, un número muuuuuyyyyy grande) a ser un número más o menos pequeño (el radio (R) de la circunferencia). Así que en el denominador de tu fórmula había un descenso brusco… ¡y por eso se producía un aumento brusco de la fuerza centrífuga! Mal asunto.
¿Qué puedes hacer entonces? Repasando tu fórmula ![]() tienes:
tienes:
- La masa (m), multiplicando. Disminuir ésta requeriría adelgazar el vehículo y sus ocupantes… y bien sabes que no es fácil.
- La velocidad (v), multiplicando (y además al cuadrado). Podrías ir más despacio, pero entonces tardarías más… y seguro que no te gusta.
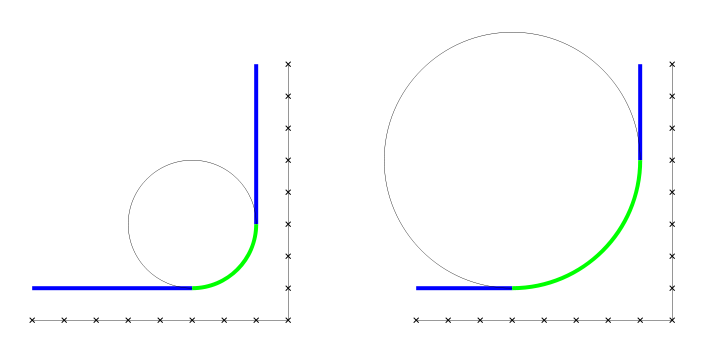
- El radio de curvatura (r), dividiendo. El de la recta es infinito, no lo puedes cambiar. Sí podrías aumentar el radio de la circunferencia, pero entonces (como en la imagen anterior) las rectas serían más cortas… y seguro que tampoco te gusta.
Así que tendrás que pensar en otra posibilidad. ¿Se te ocurre algo?
Claro que sí, podrías introducir una curva de transición entre la recta y la circunferencia. Además sería genial que, en esa transición, el radio de curvatura (r) fuera disminuyendo suavemente desde el infinito (o número muuuuuyyyyy grande) de la recta hasta el radio (R) de la circunferencia.
Según tu fórmula, eso haría que la fuerza centrífuga cambiara de manera suave, en lugar de hacerlo bruscamente.
¿Así que te gustaría que el radio de curvatura (r) fuera disminuyendo a medida que la distancia (d) recorrida fuera aumentando? Espera un momento. Tienes dos cantidades… quieres que una se haga más pequeña cuando la otra se haga más grande… ¡Es lo que en el colegio llamaban cantidades inversamente proporcionales!
O sea, que quieres que el radio de curvatura (r) y la distancia (d) recorrida sean inversamente proporcionales. ¿Y cómo era eso? Ah, sí, eso significaba que su producto fuera siempre el mismo número.
¡¡¡¡TACHÁÁÁÁÁNNN!!!!
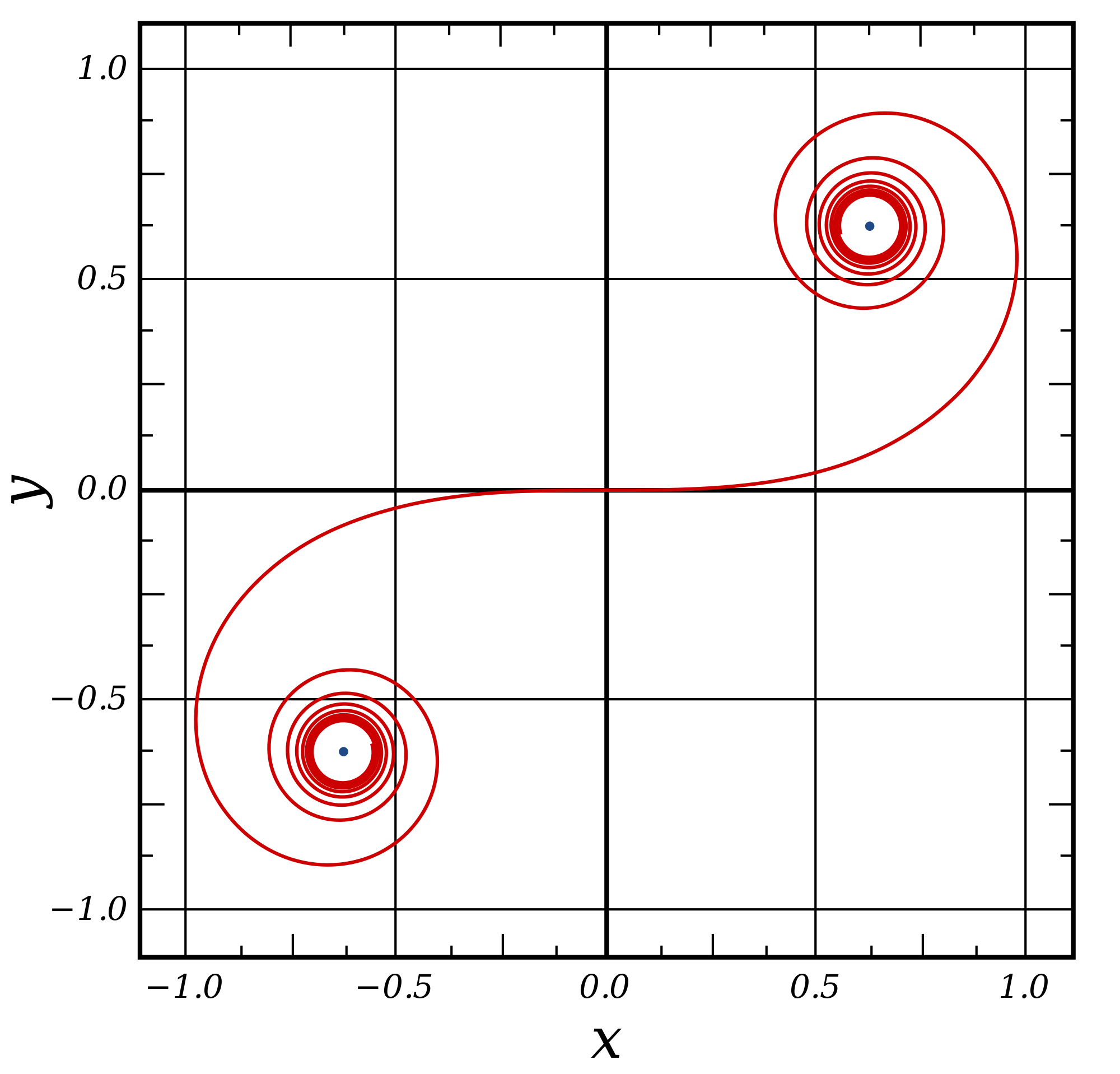
Justo esta propiedad es la que define a la curva clotoide, que ya conocían matemáticos y físicos. Su ecuación es precisamente ![]() (donde (C) es una constante, que se pone al cuadrado para facilitar las cuentas al dibujar).
(donde (C) es una constante, que se pone al cuadrado para facilitar las cuentas al dibujar).
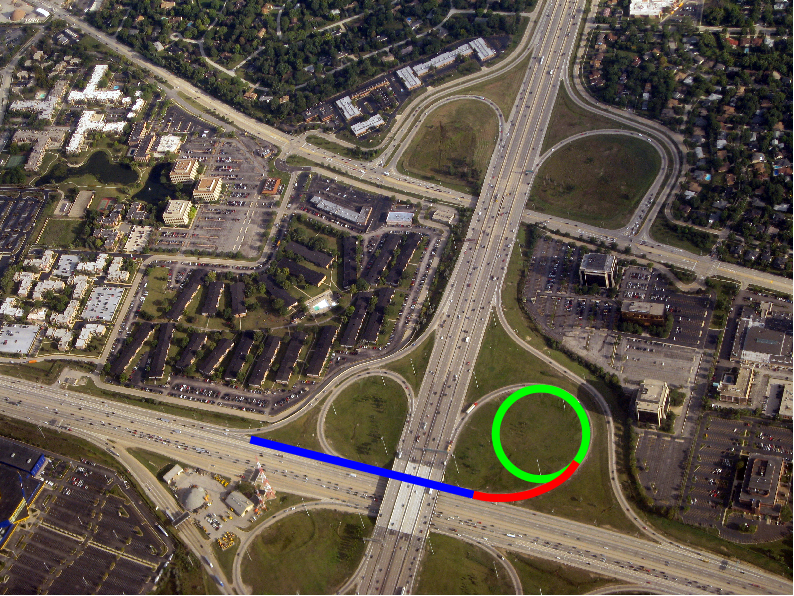
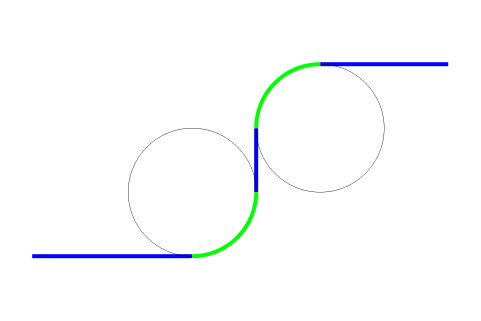
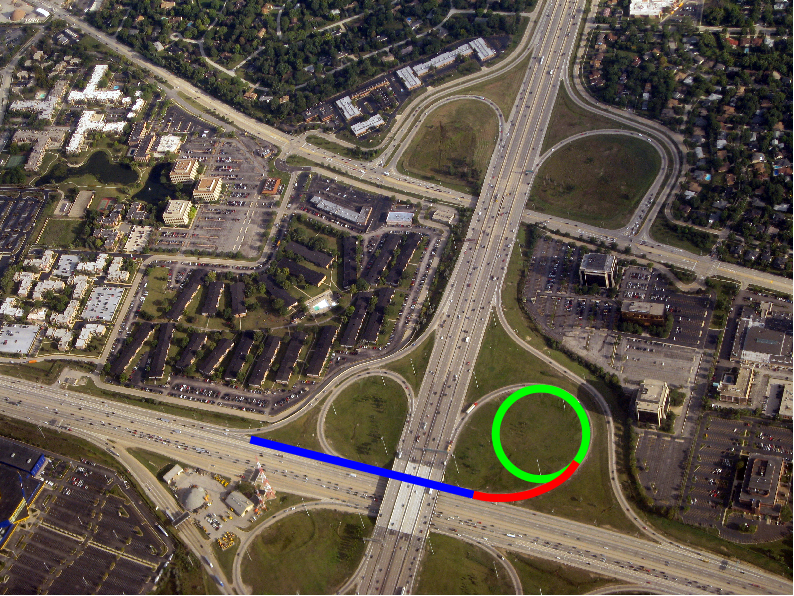
Por eso en tus carreteras y ferrocarriles las curvas suelen encadenar tramos de recta – clotoide – circunferencia – clotoide – recta. De ese modo la fuerza centrífuga va cambiando gradualmente y puedes girar el volante de forma progresiva, en vez de tener que hacerlo bruscamente.
La próxima vez que tomes una curva, no olvides que las matemáticas y la física estarán allí para ayudarte 😉
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Nota 1: Esta entrada ha llegado a portada en Menéame. ¡Gracias!
Nota 2: Esta entrada ha llegado al Olimpo en Divoblogger. ¡Gracias!
Nota 3: Esta entrada participa en la edición 4.1231056256 del Carnaval de Matemáticas, cuyo blog anfitrión es Cuentos Cuánticos.
Nota 4: Esta entrada ha resultado ganadora de la XLVIII Edición del Carnaval de la Física, cuyo blog anfitrión es La Aventura de la Ciencia.
Nota 5: Esta entrada está dedicada a los lectores de km77 que soportan otras entradas menos automovilísticas. Muy en especial a DavidVR, que fue quien me propuso escribir sobre la clotoide. ¡Gracias!
Para saber más:
Todo lo anterior sirve también, dándole la vuelta, para la salida de una curva.
Además de en carreteras y vías férreas más o menos convencionales, las clotoides se utilizan también en circuitos de velocidad y en montañas rusas.
Al parecer el primero en estudiar la clotoide fue el matemático suizo Jakob Bernoulli, en 1694, en el contexto de un problema de elasticidad. Dicho problema fue resuelto en 1744 por el matemático y físico suizo Leonhard Euler, quien dio una caracterización de la curva. Alrededor de 1818, el físico francés Augustin-Jean Fresnel redescubrió la clotoide al estudiar la difracción de la luz, y obtuvo una parametrización de esta curva mediante integrales, equivalentes a las de Euler. En 1874, el físico francés Marie Alfred Cornu consiguió usar esa expresión para dibujar la curva de manera precisa. Y más tarde, en 1890, fue el ingeniero estadounidense Arthur Talbot quien redescubrió una vez más la clotoide, inmerso ya en la búsqueda de una curva de transición para vías férreas. Si quieres saber más sobre su historia, puedes consultar el artículo The Euler spiral: a mathematical history de Raph Levien.
Por lo anterior, la clotoide se conoce también como espiral de Cornu o espiral de Euler. Si quieres más detalles sobre la clotoide y sus ventajas, quizá te interese también esta entrada de Luis González o el artículo Una aproximación a la curva de transición clotoide vista desde Mathematica de Luís Blanch, Emilio Checa y Josefa Marín.
Aunque la clotoide resulta ser la que mejores propiedades muestra, también se han considerado otras posibles curvas de transición, como la radioide de cuerdas (lemniscata de Bernoulli) o la radioide de abscisas (óvalo de Cassini). Como documento histórico, puede interesarte consultar Algunas notas sobre las curvas de las carreteras, publicado en 1929 en la Revista de Obras Públicas.
Todo lo anterior trata del diseño en 2D, pero las carreteras y las vías se construyen en 3D. Por tanto en su diseño entran en juego factores adicionales, como por ejemplo los peraltes. Si quieres más detalles sobre el trazado de carreteras, puedes consultar los apuntes de Josep Pedret Rodés. También puedes leer el Capítulo 3 de la tesina de Víctor Balboa Caparrós.
Si quieres saber cómo se calcula el radio de curvatura para una curva cualquiera, puedes consultar el artículo de la Wikipedia sobre la circunferencia osculatriz.
Si te ha gustado lo de encadenar tramos rectos y arcos de circunferencia, como en las cintas transportadoras, puedes probar a usar el tipo de letra Conveyer Belt Font, desarrollado por mis colegas Erik Demaine, Martin Demaine y Belén Palop. También puedes leer el artículo Conveyer-Belt Alphabet.
Por último, quizá te interese leer otras entradas sobre la clotoide. Puedes leer ésta en Sacit Ametam o ésta otra en La mesa cero del Blasco. También ha aparecido, entre otras curvas, en una entrada de Mati y sus mateaventuras. Y si te gusta Regreso al futuro, no dejes de leer esta entrada en Taringa donde Doc le explica varias curvas a Marty McFly.
Imágenes:
La imagen de la clotoide en el cruce de autovías es un añadido propio a una imagen de Doc Searls en Flickr (y se distribuye con la misma licencia que la imagen original). La imagen de la clotoide completa está tomada de Wikimedia Commons. La imagen de la montaña rusa está tomada de Jeremy Thompson en Flickr. El resto de imágenes son de creación propia.




Deja una respuesta