Piensa en un cubo. Seguro que sabes distinguir entre ancho, alto y profundo, que son las tres dimensiones de nuestro mundo 3D. ¿Quieres saber cómo sería el cubo con una dimensión más, que vive en 4D? Si sigues leyendo descubrirás que es más fácil de lo que pensabas y, quién sabe, quizá te animes a explicarlo en un bar… te aseguro que se puede, porque yo lo he hecho 😉
Vamos a empezar con un mundo formado por un solo punto que, aunque no lo sepa, es un cubo en ese mundo 0D. Como debe de ser muy aburrido vivir tan solo, vamos a añadir una dimensión más a su mundo y colocar otro punto igual a su derecha, a distancia 1. Para distinguirlos, al punto original le llamamos (0) y al punto nuevo le llamamos (1).
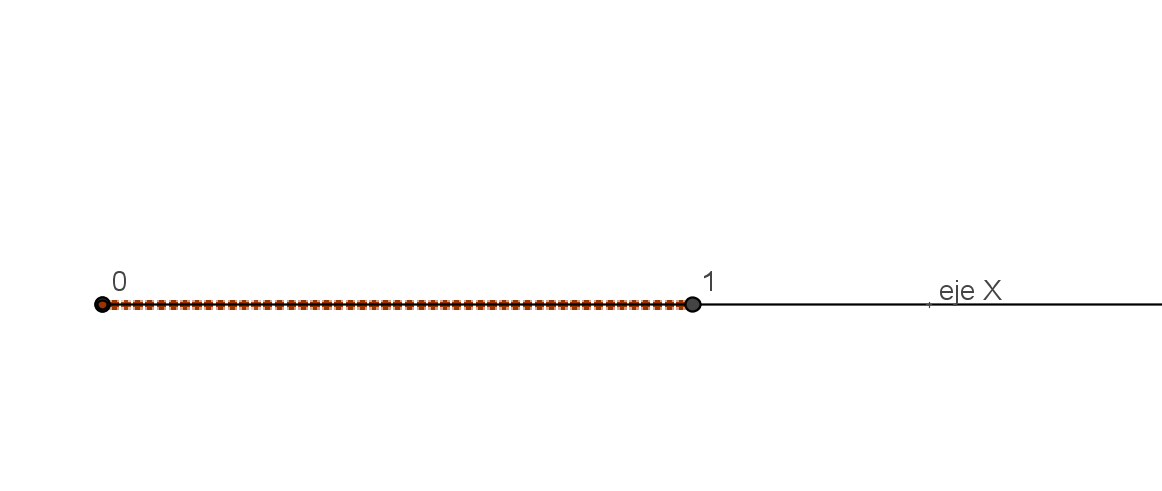
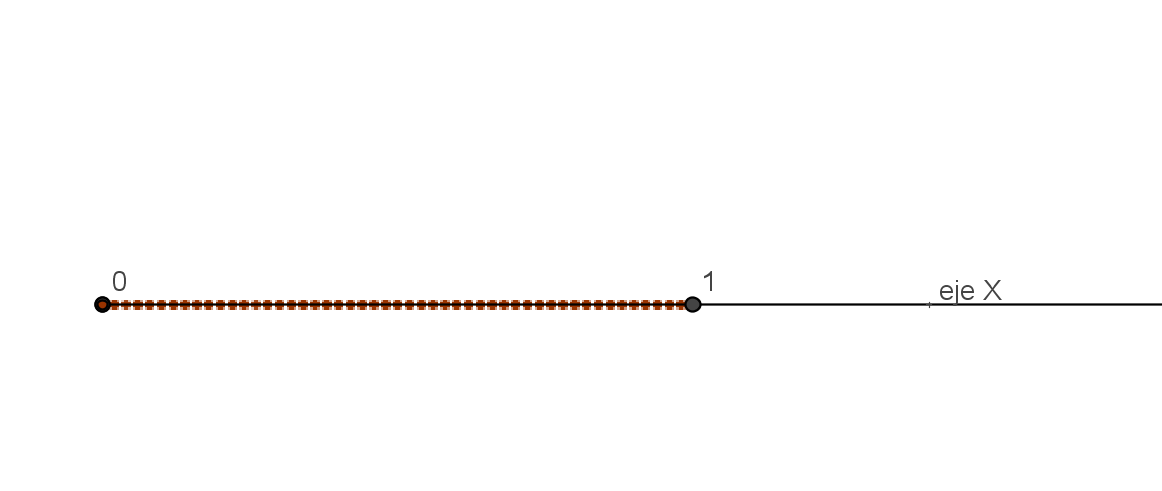
Ahora (0) y (1) son los vértices de un segmento, formado por todos los puntos entre ellos. Y aunque tampoco lo sabe, este segmento es un cubo en ese mundo 1D.
Y una vez que tenemos el cubo en 1D, podemos añadir una dimensión más y colocar otro segmento igual por encima, a distancia 1. Los dos segmentos tienen vértices (0) y (1), así que para distinguirlos vamos a poner detrás un (color{red}{0}) a los vértices del segmento original (que ahora serán (0color{red}{0}) y (1color{red}{0})) y pondremos detrás un (color{red}{1}) a los vértices del segmento nuevo (que ahora serán (0color{red}{1}) y (1color{red}{1})).
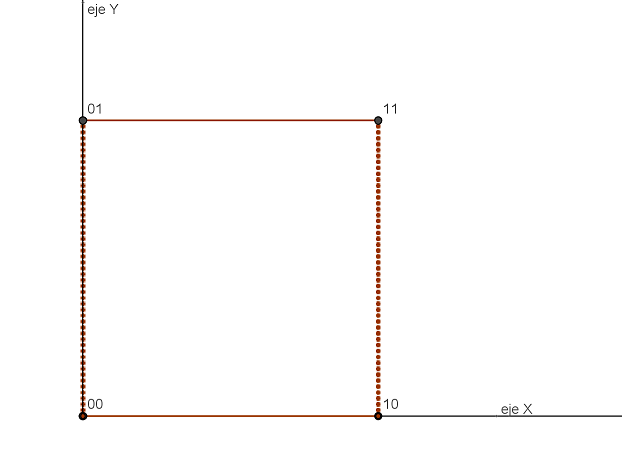
Lo siguiente, claro, es añadir la tercera dimensión y colocar otro cuadrado igual por delante, a distancia 1. Como las pantallas suelen ser 2D, poner este cuadrado por delante haría que no se pudiera distinguir del anterior, así que usaremos el truco habitual y lo pondremos un poco desplazado para que parezca que está delante.
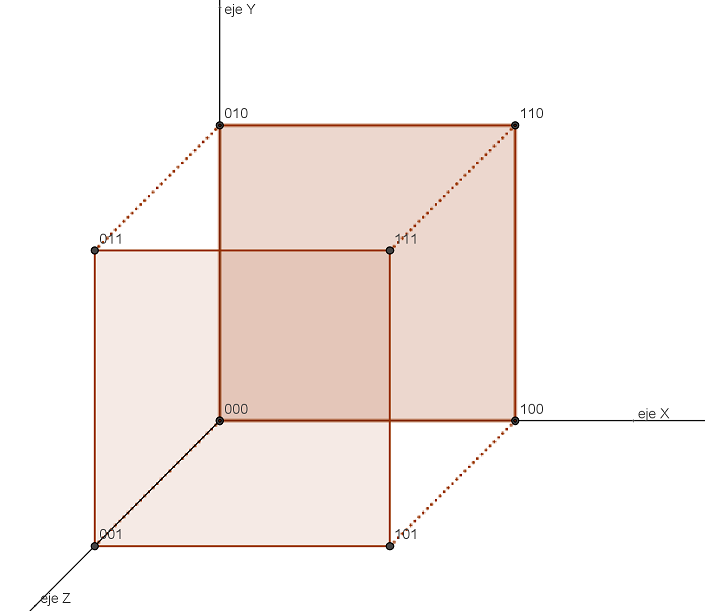
Como los dos cuadrados tienen vértices (00), (10), (01) y (11), para distinguirlos hemos puesto detrás un (color{red}{0}) a los vértices del cuadrado original (que ahora serán (00color{red}{0}), (10color{red}{0}), (01color{red}{0}) y (11color{red}{0})) y un (color{red}{1}) a los vértices del cuadrado nuevo (que ahora serán (00color{red}{1}), (10color{red}{1}), (01color{red}{1}) y (11color{red}{1})).
Ahora (000), (100), (010), (110), (001), (101), (011) y (111) son los vértices de un cubo, formado por todos los cuadrados entre ellos. Y no sólo es un cubo en su mundo 3D, además es famoso.
¡Y ahora es cuando necesitamos una cuarta dimensión! Si has seguido el hilo de lo anterior, te estarás imaginando que necesitamos esa cuarta dimensión para poner un cubo como que el que tenemos en 3D. ¿Qué te parece si usamos como dimensión el tamaño (suena razonable) y el cubo nuevo es más grande que el original? Algo así:
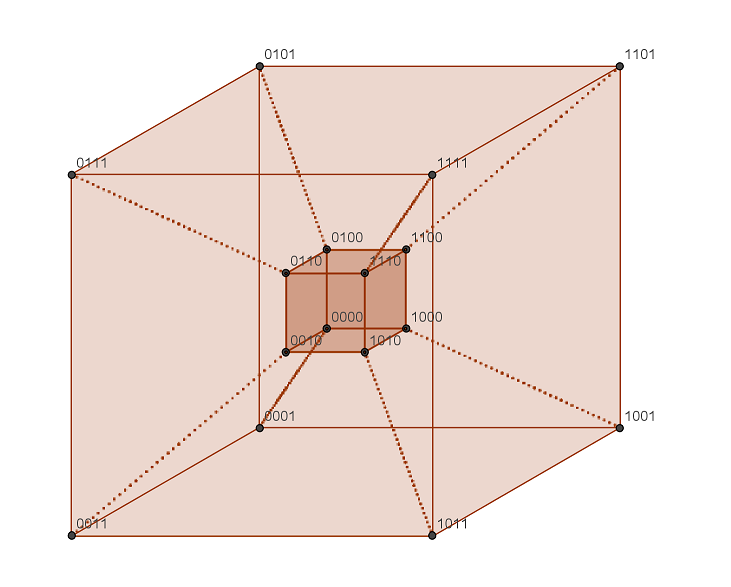
Igual que antes, a los vértices del cubo original les hemos puesto detrás un (color{red}{0}) y a los del cubo nuevo les hemos puesto detrás un (color{red}{1}) (no vamos a escribirlos todos, porque ya serían muchos…) Esos 16 vértices son los vértices del cubo en 4D, que está formado por todos los cubos entre el original y el nuevo.
¡¡¡¡Tacháááánnnn!!!
¿Cómo? ¿Que todavía no lo tienes claro? No te preocupes, vamos a intentar verlo de otra manera.
Si vuelves a mirar el cubo en 2D, verás que sus vértices son cadenas de (0)s y/o (1)s (bits para los amigos) de longitud 2. Y que además un vértice está unido a otro cuando las cadenas de ambos vértices se diferencian en un solo bit. (De hecho para el cubo en 1D, pasa lo mismo pero con cadenas de longitud 1). Por ejemplo, el (00) sí está unido al (10) y al (01), pero no al (11) porque les diferencian dos bits.
Ahora mira otra vez el cubo en 3D; sus vértices son cadenas de bits de longitud 3 y también se cumple que dos vértices están unidos cuando sus cadenas tienen un solo bit de diferencia. Así, el (000) sí está unido al (100), al (010) y al (001), pero no al (101) porque les diferencian dos bits, ni al (111) porque les diferencian tres bits.
¿Y nuestro presunto cubo en 4D? Pues resulta que sus vértices son cadenas de bits de longitud 4 y de nuevo dos vértices se unen cuando sus cadenas difieren sólo en un bit. Como ejemplo, puedes comprobar que el (0000) sí está unido al (1000), al (0100), al (0010) y al (0001), pero no al (1010), del que le diferencian dos bits, ni al (1011), del que le diferencian tres bits, ni al (1111), del que le diferencian cuatro bits.
Así que no te he engañado y la figura anterior es realmente un cubo en 4D. ¿Fácil, verdad?
Para saber más:
En realidad la figura del cubo en 3D es un diagrama de Schlegel, que permite representar en nuestra pantalla 2D una figura 3D. De manera análoga, para representar el cubo en 4D primero hacemos un diagrama de Schlegel para representarlo en 3D y, posteriormente, hacemos un diagrama de Schlegel de esta representación, para poder dibujarlo en la pantalla 2D.
A los poliedros en dimensión general (d) se les llama politopos. Para un politopo con (n) vértices en dimensión (d) se puede obtener una representación en (mathbb{R}^{n-d}) usando su diagrama de Gale. Esta técnica es más compleja, pero por ejemplo permitiría representar en el plano (mathbb{R}^{2}) cualquier figura en 4D que tenga 6 vértices.
La idea anterior para las cadenas de bits se puede continuar hasta la dimensión (d) que se quiera. El grafo que se obtiene con los vértices y las aristas unidos de esta manera se conoce como grafo hipercubo y está relacionado con los códigos Gray, que se utilizan para digitalizar la medición de ángulos.
Puedes seguirnos en Twitter, Facebook y Google +.
Nota 1: Esta entrada participa en la edición 3.141592653 del Carnaval de Matemáticas cuyo blog anfitrión es Que no te aburran las M@TES.
Nota 2: Esta entrada ha llegado a portada en Menéame.
Nota 3: Esta entrada ha llegado al Olimpo en Divoblogger.


Deja una respuesta