Puede que ya hayas oído hablar de Paul Erdős, un matemático famoso por proponer problemas muy fáciles de explicar, con aspecto inofensivo, pero que luego resultan endiabladamente difíciles de resolver. El problema de esta entrada es uno de ellos. Es tan fácil de explicar que podrás buscar una solución mientras chapoteas en la piscina, pero es tan difícil de resolver que nadie lo ha conseguido desde 1946.
Estás en la piscina y has terminado de leer el libro que traías. Ya hace un rato que has repasado (disimuladamente) al resto de bañistas y empiezas a aburrirte. Distraído, te descubres con la mirada fija en las ondas que el chapoteo de un niño ha dejado en el agua.
Como no se te ocurre nada mejor que hacer, decides sentarte un rato en el borde de la piscina. Mientras chapoteas con el pie, vuelves a quedarte mirando las ondas que se forman. Tras practicar un par de veces, le encuentras el truco y eres capaz de dar un golpe seco con el que las ondas forman circunferencias concéntricas, casi perfectas.
Orgulloso, contemplas tus ondas y te da por fijarte en que avanzan tocando en dos puntos el borde de la piscina:
Aprovechas un momento en que la piscina se vacía para probar un golpe más fuerte, con el que consigues que las ondas atraviesen toda la piscina. Y descubres, entusiasmado, que las ondas siempre chocan con el borde en dos puntos:
Por si acaso, pruebas a chapotear en varios sitios más (siempre en el borde) y compruebas que en todos ellos sucede lo mismo.
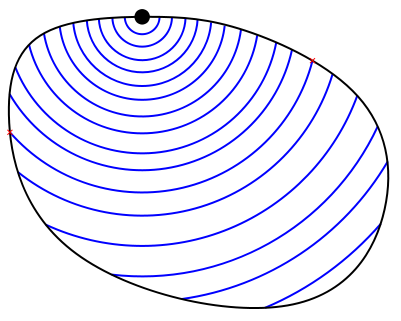
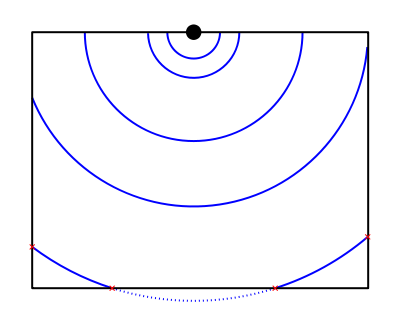
Te queda la duda de si será así en todas las piscinas, así que al día siguiente decides repetir el experimento en la piscina de natación. Te sientas en un lateral, ejecutas tu famoso golpe de pie y te fijas en que las ondas empiezan chocando con el borde en dos puntos, pero hay un momento en que pasan a chocar en cuatro puntos:
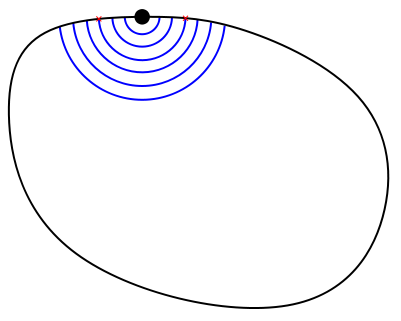
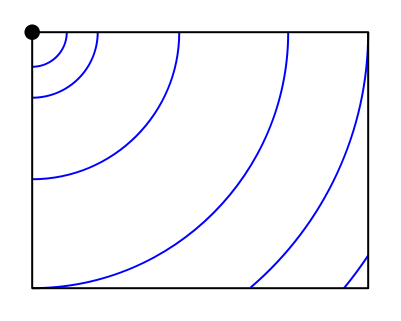
Intrigado, pruebas a chapotear en una esquina en lugar de un lateral y, para tu sorpresa, descubres que al chapotear desde allí ninguna onda choca en más de dos puntos:
Mientras vuelves a casa una pregunta salpica tu cabeza:
Si chapoteas en el borde de una piscina, ¿en cuántos puntos pueden chocar las ondas con el borde?
Esa misma noche, tomando algo en una terraza, se te ocurre preguntarle a tu amigo el que estudió arquitectura. Lo piensa un poco y su respuesta te desconcierta: «Dime cuántos puntos de choque quieres y te dibujo una piscina donde conseguirlos».
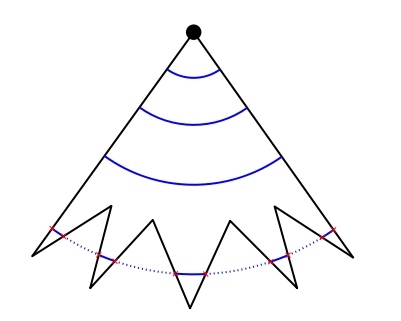
Incrédulo, le pides una piscina con diez puntos de choque y te prepara este dibujo en una servilleta:
Te abstienes de preguntarle si ha construido alguna piscina así (cosas más raras has visto) y te centras en analizar el dibujo. Al instante te das cuenta de que la clave son esos «entrantes» que parten las ondas en varios trozos, como un tajamar en un puente.
Entonces le preguntas otra vez a tu amigo el arquitecto: ¿Y qué pasaría en una piscina «sin entrantes»? Él te explica que lo de «sin entrantes» es poco riguroso y que es mejor llamarle convexo. Te enseña un ejemplo de una piscina cuyo borde sí es convexo
y otro ejemplo de una piscina cuyo borde no es convexo
Ya lo tienes más claro que el agua, así que cambias tu pregunta:
¿Si chapoteas en el borde de una piscina convexa, en cuántos puntos pueden chocar las ondas con el borde?
El bueno de tu amigo empieza a sudar más de la cuenta y, aunque le cuesta un rato, acaba reconociéndote que no sabe la respuesta.
Por suerte, en ese momento llega vuestro amigo el matemático. Él tampoco conoce la respuesta, pero la pregunta le recuerda a una entrada que ha leído hace poco en un blog de ciencia. La busca en su móvil y lo que os cuenta te parece fascinante.
Resulta que tu pregunta ya se la planteó (aunque sin pensar en piscinas) uno de los matemáticos más importantes de la historia en 1946. El tal Erdős al principio creyó que siempre se podía encontrar un sitio en el que chapotear sin que las ondas chocaran en más de dos puntos (como hiciste en tu piscina de natación).
Pero para acertar mucho también hay que equivocarse alguna vez… y en esta ocasión Erdős se equivocaba. El matemático os cuenta que, si la piscina tiene forma de triángulo acutángulo te da igual en qué punto del borde chapotees, que en algún momento tus ondas van a chocar con el borde en cuatro puntos. Termina de convencerte con una construcción interactiva.
Además resulta que matemáticos de todo el mundo siguen intentando resolver el problema. Este mismo año unos investigadores han publicado una figura (convexa) para la que, chapoteando desde cualquier punto del borde, las ondas siempre acaban chocando en seis puntos.
Antes de pedir otra ronda, vuestro amigo os aclara que esto no resuelve el problema. Nadie sabe (aún) si la respuesta es seis o si existe una forma convexa para la que ese número sea más grande.
…
Cuando un par de rondas más tarde os despedís, todos te felicitan por tu capacidad para hacerte preguntas. Vuelves a casa pensando en hacer algunos dibujos. Te encantaría batir el récord y descubrir uno en que las ondas acaben chocando con el borde en más de seis puntos. Si lo consigues, piensas, quizá te hagas famoso y puedas construir la piscina de tus sueños
Recuerda que puedes seguirnos en Twitter, Facebook y Google+.
Nota: Esta entrada ha llegado al Olimpo en Divoblogger.
Fotografías: La fotografía de las ondas en el agua está tomada de José Paulo da Silva Ferreira, en Flickr. La fotografía de la piscina convexa está tomada de Michael Coghlan, en Flickr. La fotografía de la piscina no convexa está tomada de Nayu Kim, en Flickr. La fotografía de la piscina con forma de guitarra está tomada de Wicker Paradise, en Flickr.
Para saber más:
Si no tienes claro lo que es convexo y lo que no, quizá te ayude mirar estos otros ejemplos de piscinas convexas y de piscinas no convexas.
Erdős está considerado el matemático más prolífico de la historia, junto con Leonhard Euler. Parece que Erdős publicó más artículos, unos 1525 y la mayoría junto con otros investigadores, mientras que Euler publicó más páginas, la mayoría en solitario.
Erdős también era un poco excéntrico; una buena muestra aparece en el prólogo del libro Research Problems in Discrete Geometry, donde viene a decir:
Con la Geometría Discreta me pasa como con la pornografía; no sería capaz de definirla, pero soy capaz de reconocerla en cuanto la veo.
Aunque la cita no es literal, sí subyace elegantemente en el texto. La comparación tampoco es original de Erdős, quien refiere a su uso por un juez de la Corte Suprema de los Estados Unidos.
También es interesante el epitafio que, según el libro The man who loved only numbers, escribió para sí mismo:
Finally I am becoming stupider no more.
Si tienes curiosidad sobre la vida de Paul Erdős, puedes leer la entrada que sobre él escribió Clara Grima. Si quieres saber más sobre su trabajo en matemáticas, puedes encontrar muchos de sus artículos (no he comprobado si están todos) en la página The Erdős Project, que descubrí gracias a una entrada de Gaussianos. También es muy interesante la página The Erdös Number Project, donde puedes probar a calcular tu número de Erdős (o el de tu profesor ;-)).
Si prefieres ver y escuchar a Erdős en acción, te recomiendo este vídeo en el que cuenta una broma sobre Simon Sidon. Si tienes más tiempo, puedes disfrutar de este reportaje de la BBC sobre él.
Por último, déjame decirte que esta entrada está basada en la entrada Advances on an Erdős problem on convex boundaries, que escribí para Mapping Ignorance. Allí hay mucha más información, un poco más técnica pero con la que puedes profundizar en este problema. En particular, explica un poco más sobre ese artículo publicado recientemente con una figura convexa en que las ondas siempre acaban chocando en seis puntos.







Deja una respuesta