Seguro que has oído hablar de la «velocidad de paso por curva» de un coche o una moto, pero ¿te has preguntado alguna vez cómo se calcula? Seguro que también has estudiado matemáticas pero ¿sabrías explicar a tu cuñado qué es una integral? En esta entrada usarás datos reales de telemetría del Circuito de Mónaco para entender de forma sencilla que una integral no es más que una suma, con la que puedes medir la velocidad de paso por curva. Como bonus track, el mismísimo Pedro Martínez de la Rosa nos contará cómo la miden en la Fórmula 1.
Es domingo al mediodía y estás con la familia en un bar. En la tele tienen puesta la Fórmula 1, es el Gran Premio de Mónaco y un pelón se lamenta del coche que tiene su mago favorito. Tu cuñado no tarda en sentar cátedra afirmando que «el problema es la velocidad de paso por curva, porque en las rectas cualquiera puede ir rápido». Cuando le preguntas ¿tú sabes cómo se mide la velocidad de paso por curva? se le atraganta la aceituna. Y casi se desmaya cuando le dices que vas a explicárselo y que, de paso, conseguirás que entienda de una vez qué es una integral.
Imagina que eres el ingeniero jefe de una escudería y quieres comparar la velocidad de paso de tus dos pilotos por la curva del Casino de Montecarlo. Podrías poner un hombrecillo verde con un radar en un punto de la curva, midiendo la velocidad de tus pilotos para luego comparar cuál de los dos ha pasado más rápido por allí.

Digamos que el piloto azul ha pasado a 120 km/h y el piloto rojo a 114 km/h. Comparando esas dos velocidades, está claro que en ese punto el azul ha pasado más rápido. Pero, ¿significa eso que el piloto azul ha sido el más rápido en la curva? No tiene por qué; puede ser que en otro punto distinto de la curva el rojo fuera más rápido.
Por si acaso, eliges otro punto de la curva y pones otro radar. Descubres que por este nuevo punto el piloto azul pasa a 127 km/h y el rojo pasa a 132 km/h. Allí la cosa cambia y el más rápido es el piloto rojo. Antes era el azul, ahora es el rojo,… ¿Quién demonios es el más rápido en esa curva?
Veamos; para el piloto azul tienes dos valores, 127 km/h y 120 km/h. Para el rojo tienes 132 km/h y 114 km/h. Y quieres compararlos. Una opción es calcular la velocidad media de cada piloto y compararlas.
[color{blue}{frac{127+120}{2}} quad > quad color{red}{frac{132+114}{2}}]
Si te fijas, las dos sumas están divididas por lo mismo, así que puedes olvidarte del divisor y comparar sólo las sumas, que es más fácil:
[color{blue}{127+120} quad > quad color{red}{132+114}]
Total, que si tienes en cuenta las mediciones en dos puntos, el más rápido es el piloto azul… ¿Qué pasará si pones otro radar más en un tercer punto?
Mandas para allá a otro hombrecillo verde con su radar y, un rato después, te cuenta que el piloto azul ha pasado por su punto a 147 km/h, mientras que el rojo ha pasado a 153 km/h.
Sólo tienes que sumar los tres valores y comparar:
[color{blue}{147+127+120} quad < quad color{red}{153+132+114}]
¡¡Ahora resulta que el más rápido es el piloto rojo!! Azul, rojo, azul, rojo… te estás volviendo loco.
Decides relajarte, tomar aire y pensarlo un poco. Enseguida te das cuenta de que no basta con sumar las velocidades en algunos puntos sueltos. Necesitas sumar las velocidades en todo el tramo de la curva.
Por suerte, tu equipo acaba de instalar unos sistemas de telemetría, que te envían continuamente la velocidad del coche, así que mandas de vacaciones a los hombrecillos verdes y te pones a estudiar esos datos.
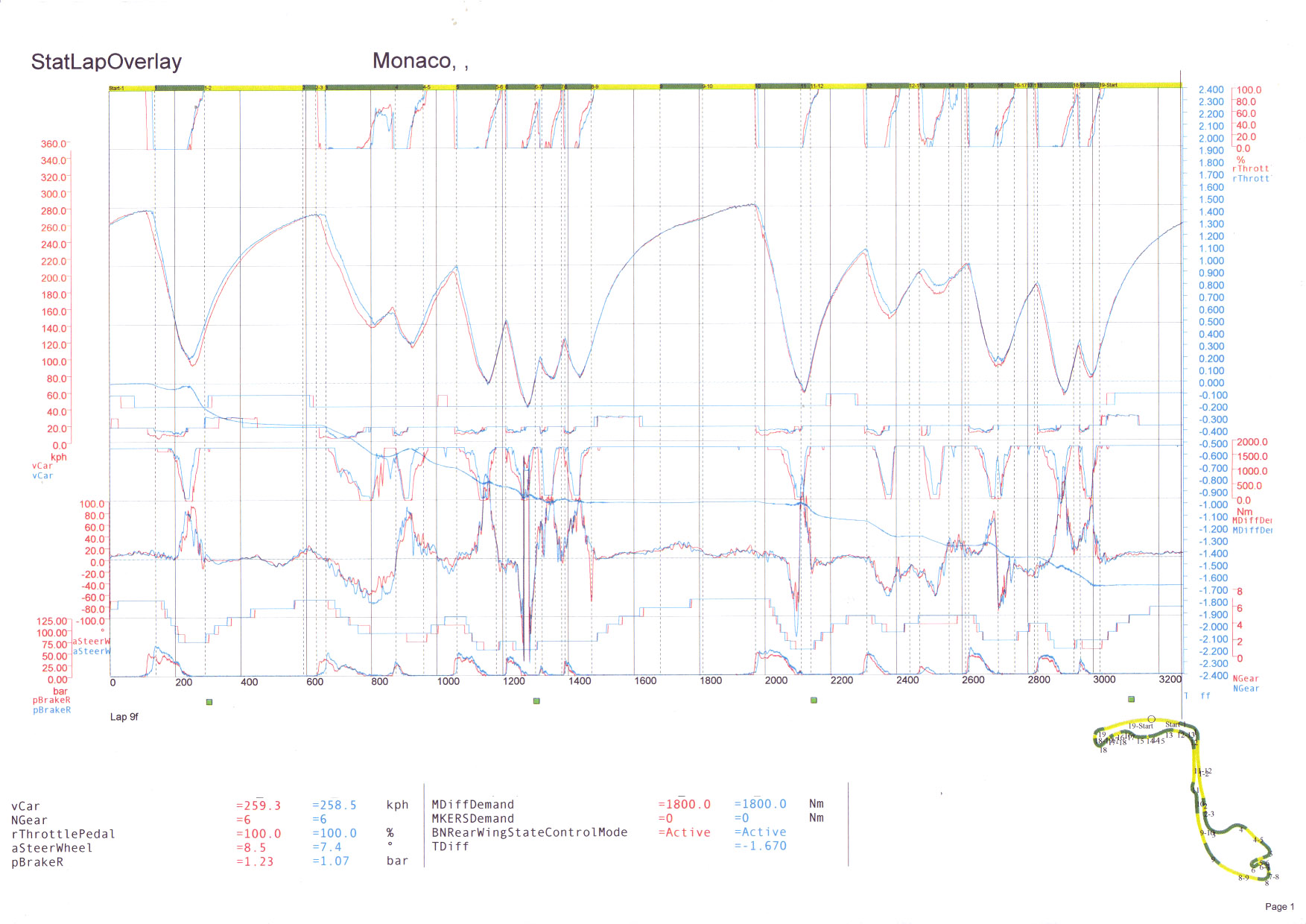
En vez de sumar unos cuantos valores sueltos, lo que quieres ahora es sumar unos valores que estás recibiendo continuamente. ¡¡Y eso es precisamente lo que hace una integral!! Una integral no es más que una «suma continua».
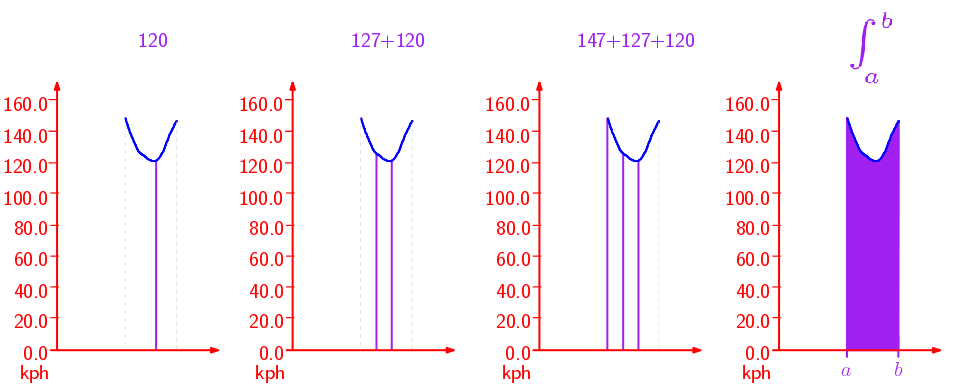
Así que haces la integral de la función de velocidad en ese tramo y ya tienes la suma de las velocidades a lo largo de la curva. Es decir, la velocidad total de paso por curva. Ahora sólo tienes que calcular la integral para un piloto y para el otro; comparándolas sabrás cuál de ellos es más rápido. [EDITADO] Lo que pasa es que esa suma de velocidades no es tan representativa como parece; en la entrada posterior a ésta tienes explicado el porqué.
Si se lo explicas así, seguro que tu cuñado lo entiende… aunque puede que aún tenga algo que decir 😉
Bonus track:
Nuestro anfitrión Javier Moltó ha preguntado cómo calculan la velocidad de paso por curva a Pedro Martínez de la Rosa, piloto de pruebas de la Scuderia Ferrari de Fórmula 1 y presidente de la Grand Prix Drivers Association. Éste nos ha honrado con las siguientes declaraciones, especiales para Cifras y Teclas:
Sobre tus preguntas, cuando hablamos de velocidad de paso por curva nos referimos a la velocidad mínima de paso por curva, que suele coincidir con el vértice de la curva.Para comprobar esta velocidad, miramos la telemetría y en la traza de la velocidad, cogemos la más baja de cada curva. Así las sabemos.Lo más importante de esta traza de velocidad es su forma, no la cifra en sí. Es decir, cómo/cuándo reduces velocidad entrando en la curva y cuándo empiezas a dar gas. Puedes tener una velocidad de paso muy alta pero si has frenado muy tarde y no consigues dar gas pronto, no te sirve de nada…
Pedro Martínez de la Rosa (Comunicación personal, octubre de 2013).
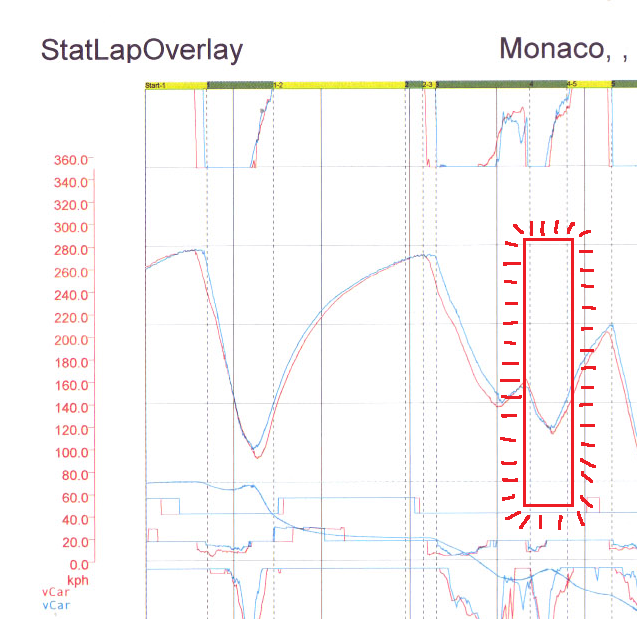
Si abres la imagen anterior con los datos de telemetría, comprobarás que en casi todos los tramos se observa a simple vista que el piloto azul es más rápido que el rojo. Pero hay un tramo en el que ambas gráficas se entrelazan y no resulta tan fácil decidirlo; es precisamente la curva del Casino (curva 4) de la que hemos tomado los datos de nuestro ejemplo.
Allí la velocidad más baja del piloto rojo es menor que la más baja del piloto azul. Pero como las curvas están entrelazadas, tendríamos que mirar su forma. Para eso podemos usar la integral, que coincide con el área bajo la curva. Si haces zoom y te fijas en cuál de las dos curvas tiene más área por debajo, parece que efectivamente el azul es el más rápido… pero yo calcularía la integral por si acaso (manías de ser matemático y no ingeniero ;-)). [EDITADO] Como antes, ese área no es tan representativa como parece y en la entrada posterior a ésta tienes explicado el porqué.
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Nota 1: Esta entrada a llegado a portada en Menéame. ¡Gracias!
Nota 2: Esta entrada ha llegado a portada en Divúlgame. ¡Gracias!
Nota 3: Esta entrada ha llegado al Olimpo en Divoblogger. ¡Gracias!
Nota 4: Es un verdadero lujo contar con el testimonio de alguien como Pedro Martínez de la Rosa en un artículo de divulgación matemática. Ojalá sirva para que las matemáticas lleguen a más gente. También es un lujo tener el apoyo de alguien como Javier Moltó, sin cuyas gestiones esto no habría sido posible. Quiero agradecérselo infinitamente a ambos y lo menos que puedo hacer es dedicarles humildemente esta entrada.
Nota 5: Esta entrada participa en la edición 4.1231056 del Carnaval de Matemáticas, cuyo anfitrión es el blog Scientia.
Para saber más:
Si ya has entendido qué es una integral y ahora lo que buscas es cómo resolverla, te recomiendo los materiales de Juan Medina Molina en lasmatematicas.es.
Si quieres ir a la fuente original de los datos de telemetría, puedes encontrarlos, analizados con todo lujo de detalles, en la entrada Telemetry and Data Analysis Introduction del blog ScarbsF1 (muy recomendable si quieres un punto de vista técnico sobre la Fórmula 1). Hay una entrada similar en español, algo menos detallada.
Si lo que te interesa es saber cómo ir rápido en una curva (por favor te lo pido, inténtalo sólo en condiciones seguras para todos), puedes leer la entrada sobre trazada en Wikipedia (en inglés) o ésta otra en drivingfast.net (también en inglés).
Si quieres saber más sobre Ayrton Senna, la entrada sobre él en la Wikipedia es bastante completa. Mantiene el récord de victorias en el Gran Premio de Mónaco, que ganó en un total de 6 ocasiones, 5 de ellas consecutivas. Si quieres, puedes ver una vuelta a este circuito desde su monoplaza.
Si sólo conoces la Fórmula 1 en tiempos de Fernando Alonso, puedes leer esta entrada en Jot Down de Guillermo Ortiz para hacerte una idea de cómo era antes.
Imágenes:
La imagen de Ayrton Senna pasando por la curva del Casino de Montecarlo está tomada del Instituto Ayrton Senna, en Flickr. La imagen de la telemetría está tomada, con su permiso (many thanks!), del blog ScarbsF1.



Deja una respuesta