Llega el año nuevo y, como siempre, necesitas algo original para destacar entre la avalancha de felicitaciones. Puedes usar que 2014 es un número esfénico entre esfénicos (porque 2013 y 2015 también lo son), pero eso ya lo leíste el año pasado. Para este año te propongo buscar un papel cuadriculado, dibujar caminos y contar cuadraditos. ¿Te apetece pasarlo bien y de paso aprender matemáticas?
¿Cuánto hace que no usas papel cuadriculado? Quizá tengas alguno por casa, o puede que no hayas vuelto a usarlo desde tus años del colegio (siempre puedes imprimirlo). Si quieres pasar un rato entretenido, hazte con uno y busca algo que pinte. Te propongo un juego:
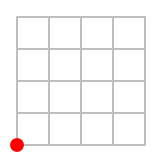
(1) Dibuja un punto en la esquina inferior izquierda de tu papel cuadriculado.
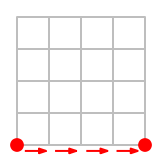
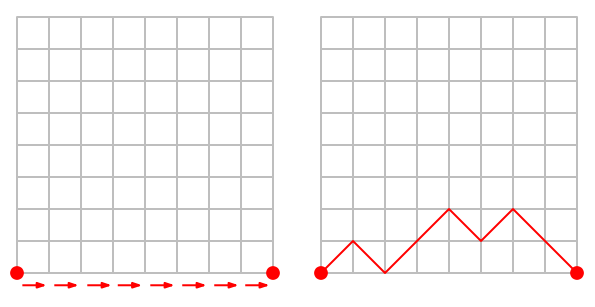
(2) Elige un número (natural) y dibuja otro punto empezando en el anterior y dando ese número de pasos hacia la derecha. Por ejemplo, si eliges el número 4 tendrás esto:
(3) El juego consiste en dibujar caminos entre esos dos puntos, dando tantos pasos como el número que hayas elegido. En nuestro caso, caminos de 4 pasos. La gracia del juego es que sólo puedes dar pasos de estos tipos:
- Paso en horizontal hacia la derecha (un lado de cuadradito).
- Paso en diagonal hacia arriba (una diagonal de cuadradito).
- Paso en diagonal hacia abajo (una diagonal de cuadradito).
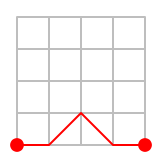
Y, por supuesto, no puedes salirte del papel por debajo. Como ejemplo, el camino de la siguiente figura es «derecha – arriba – abajo – derecha»:
¿Te animas a intentar dibujar todos los caminos posibles? Venga, inténtalo.
Te voy a dar una pista; son nueve.
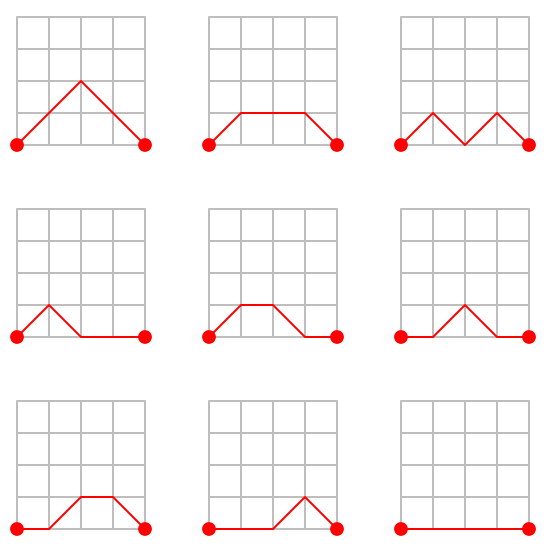
¿Ya los tienes? Seguro que has dibujado estos nueve caminos:
A los caminos construidos con este juego se les llama caminos de Motzkin (por el matemático israelo-estadounidense Theodore Motzkin). Para cada número (n) que hayas elegido en el paso (2) tendrás una cantidad distinta de caminos, y a esa cantidad se le llama (n)-ésimo número de Motzkin.
En nuestro ejemplo, hemos usado (n=4) y hemos obtenido 9 caminos de Motzkin, así que nuestro 9 es el 4º número de Motzkin. Si escribimos en ese orden los números de Motzkin, obtenemos la siguiente sucesión:
1, 2, 4, 9, 21, 51, 127, 323, 835, 2188,…
Como ves, el 2014 no forma parte de esta secuencia, así que no es un número de Motzkin… pero no te desanimes, que enseguida lo verás aparecer. Para ello sólo necesitas medir el área debajo de cada camino.
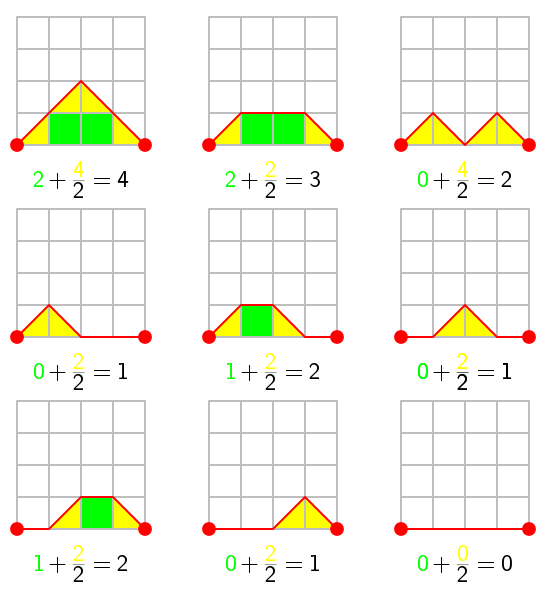
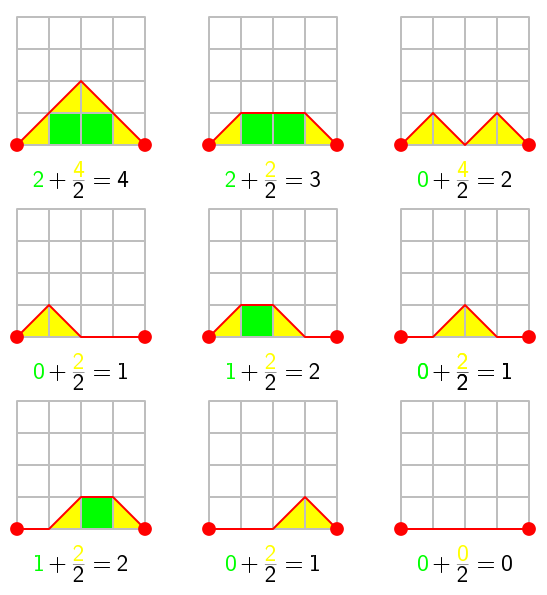
Ya sabes que para medir el área debajo de una gráfica se suele utilizar una integral. Pero las cosas con papel cuadriculado resultan más sencillas y aquí sólo tienes que contar la cantidad de cuadraditos debajo de tus caminos. Es fácil, porque sólo aparecen cuadraditos enteros o medios cuadraditos:
Ahora puedes sumar todas estas áreas bajo los caminos de Motzkin de longitud 4, y te saldrá el número 16. Puedes hacer la suma de áreas para todos los caminos de Motzkin de longitud 1, luego la suma para los de longitud 2, después para los de longitud 3, etc… y te saldrán estos números
0, 1, 4, 16, 56, 190, 624, 2014, 6412,…
que forman la sucesión de áreas bajo caminos de Motzkin (nuestro 16 es el 4º término). ¡¡Y aquí tienes el 2014 que buscabas!! Es el 8º término de la sucesión, así que corresponde a la suma de áreas bajo los caminos de Motzkin de longitud 8.
Si quieres asegurarte, tendrías que dibujar todas las posibilidades con longitud 8… pero resulta que son 323. Así que casi es mejor mirarlo en la sucesión A057585 de la OEIS (ésta es la sucesión de áreas, la de números de Motzkin es la A001006). Otra opción sería mirar la página dedicada a caminos de Motzkin en el Wolfram Demonstrations Project.
Comprobarás que la última vez que un año fue suma de áreas bajo caminos de Motzkin fue en 624 y que esto no volverá a suceder hasta 6412, así que el único año con esta propiedad que podamos vivir será este 2014. Ahora lo que hace falta es:
¡Que tengas un muy feliz año 2014, suma de áreas de Motzkin!
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Para saber más:
Antes has calculado el área contando cuadraditos, pero hay otra manera muy interesante de hacerlo. Para ello sólo tienes que «cerrar» tu camino y luego usar el Teorema de Pick en el polígono resultante. Según este teorema, sólo tienes que contar:
- El número de vértices de la cuadrícula que quedan dentro del polígono.
- El número de vértices de la cuadrícula que quedan en el borde del polígono, dividido por 2.
y luego restarle 1 a la suma de esas dos cantidades.
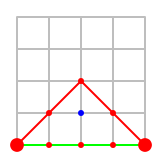
Por ejemplo, para el camino «arriba – arriba – abajo – abajo» tendríamos 1 punto dentro del polígono y 8 puntos en el borde, así que el área sería 1+8/2-1=4, que coincide con la que se obtiene contando cuadraditos.
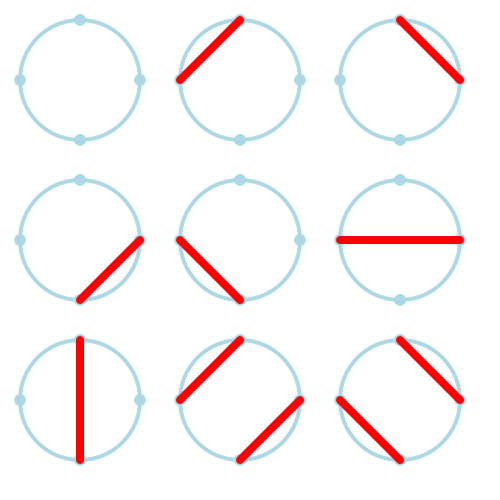
Además de contando caminos, los números de Motzkin se pueden calcular dibujando (n) puntos en una circunferencia y contando cuántas posibilidades hay de dibujar cuerdas sin que una se toque con otra (ni siquiera en los puntos). Para (n=4) hay, como antes, 9 posibilidades:
Los caminos de Motzkin tienen un «pariente» llamado caminos de Dyck con el que se obtienen unos números distintos, los números de Catalan (que dejaremos para otra ocasión). También están relacionados los números de Delannoy y los números de Schröder, para los que también puedes encontrar información (y algunos dibujos) en esta página de Robert Dickau. Si te animas, puedes intentar dibujar los 21 caminos de Motzkin de longitud 5 y después comprobar en su página la solución.
Por último, quizá esto de unir puntos sobre un papel cuadriculado te haya recordado a aquel juego de cerrar cuadrados al que jugabas en el colegio (parece que se conoce como timbiriche). Si quieres rememorar viejos tiempos, puedes jugar desde tu navegador, tu dispositivo Android, tu dispositivo iOS, o tu dispositivo Windows. ¡Disfruta!
Imágenes: Todas las imágenes son de creación propia, salvo la de las cuerdas entre cuatro puntos sobre la circunferencia, que es de Robertd en Wikimedia Commons.


Deja una respuesta