El número Pi lleva siglos fascinando a generaciones enteras, pero todavía esconde intrigantes misterios. Por ejemplo, saber si sus decimales se comportan como si fueran aleatorios. Una de las técnicas para estudiar esto consiste en traducir cada uno de esos números a un movimiento «izquierda», «derecha», «adelante» o «atrás» y dibujar el rastro de este baile de la yenka. Además de obtener imágenes bonitas, de un vistazo podrás comparar Pi con otros números.
Como pasa con las personas, hay números más diáfanos y otros más enigmáticos. Uno de los que mayor interés despiertan es, sin duda, el número Pi. Lleva siglos fascinando a generaciones enteras y todavía esconde intrigantes misterios. Por ejemplo, ¡¡aún no se sabe si el 3 aparece infinitas veces entre sus infinitos decimales!!
Esta pregunta está relacionada con otra que ha obsesionado a los matemáticos durante siglos; si Pi es un número normal. En la entrada anterior «No es seguro que todo el universo esté contenido en Pi» tienes una explicación más detallada pero, a grandes rasgos, la cuestión es si los decimales del número Pi «se parecen» a una ristra de números aleatorios, como los que te saldrían al tirar un dado infinitas veces.
Eso de que una cosa «se parezca» a otra suena muy poco matemático, ¿verdad? En realidad hay varias maneras de medir ese parecido con precisión. Y en esta entrada descubrirás otra manera, menos precisa, pero muy visual y fácil de entender.
Para ello solo necesitarás unos pocos ingredientes. Lo primero es buscar un buen montón de decimales del número Pi. Los ordenadores nos han ayudado mucho y hoy en día se conocen unos
![]()
Lo segundo es una manera de traducir esos decimales a movimientos. Una forma fácil de hacerlo sería conectar a tu pantalla un joystick con diez posiciones, y asociar cada número del 0 al 9 con un movimiento del joystick. Pero diez posiciones son muchas para recordar qué movimiento corresponde a cada número. Sería más fácil teniendo solo cuatro movimientos, «izquierda», «derecha», «adelante» y «atrás».
Y aquí llega el tercer (y último) ingrediente. Que al escribir el número Pi aparezcan solo cuatro números, en lugar de diez. Espera un poco… ¿eso no te suena de algo? Seguro que en algún momento te explicaron (y quizá sufriste) cómo hacer un cambio de base. Si no te acuerdas puedes repasarlo, pero si no tienes tiempo también puedes usar alguna herramienta para hacer cambios de base.
Resulta que el número Pi en base 10 tiene esta pinta
[3.141592653589793238462643383276ldots]
pero en base 4 tiene esta otra
[3.02100333122220202011220300203103010301212022023123ldots]
Ahora ya solo te falta identificar cada número con un movimiento. Por ejemplo
[0leftrightarrowtext{Derecha} quad 1leftrightarrow text{Arriba} quad 2leftrightarrowtext{Izquierda} quad 3leftrightarrowtext{Abajo}]
Si quieres que la imagen quede más bonita, puedes ir cambiando el color a medida que vas dando pasos. Así también podrás distinguir el principio y el final del baile. Por ejemplo, puedes ir recorriendo el espectro visible
[text{Rojo}rightarrowtext{Anaranjado}rightarrowtext{Amarillo}rightarrowtext{Verde}rightarrowtext{Azul}rightarrowtext{Violeta}rightarrowtext{Rojo}]
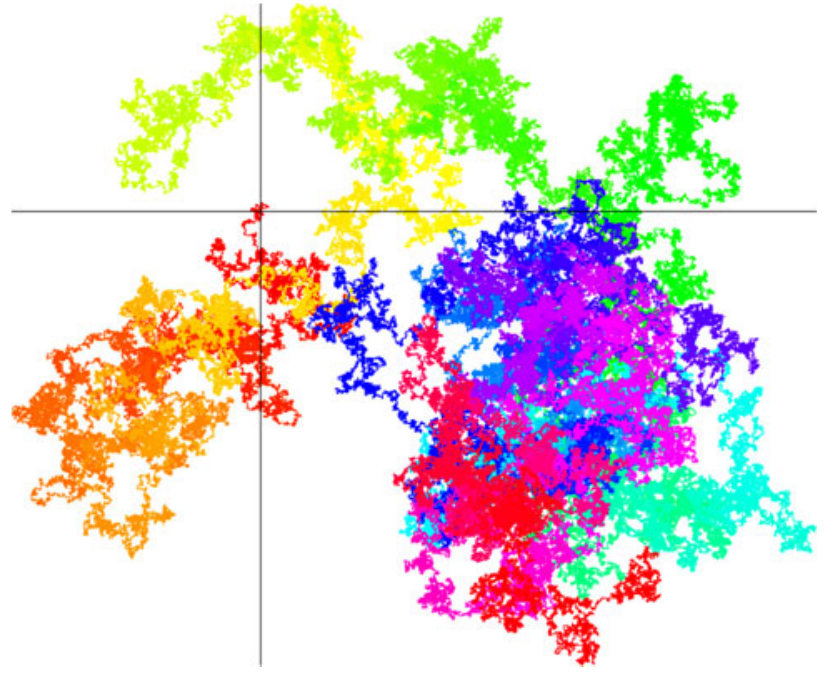
Si haces esto con los primeros (10^{11}) dígitos de Pi en base 4, obtendrás algo parecido a la siguiente imagen, generada por Francisco Javier Aragón Artacho tras un mes de computación con hasta 20 procesadores trabajando en paralelo. Está considerada una de las mayores imágenes matemáticas creadas hasta la fecha y tiene un tamaño de (372,224 times 290,218) píxeles, en total 108.03 gigapíxeles. Te recomiendo encarecidamente que la explores en Gigapan, donde puedes hacer movimientos y zoom, e incluso comprar una impresión si te gusta.
Pero recuerda que no estabas haciendo esto solo para tener una imagen bonita… Querías saber si Pi se comportaba como si fuera aleatorio. Una forma fácil sería comparar esta imagen con la de un número que sí sea aleatorio. Seguro que no tienes tiempo (ni ganas) para tirar un dado un millón de veces, pero puedes usar un número pseudo-aleatorio que es lo más parecido que se puede conseguir con un ordenador.
Y eso hicieron Francisco Javier y sus coautores en su artículo Walking on Real Numbers, generando un número con (10^6) dígitos en base 4 para el que obtuvieron esta imagen
Si comparas la imagen de Pi con la de este número pseudo-aleatorio, comprobarás que en ninguna de las dos se aprecia un patrón, que en ambas el movimiento parece más bien errático (que no pasaría un control de alcoholemia, vamos). Al contrario de lo que pasa para el siguiente número racional
Sus pasos son firmes y siguen una ruta bien marcada. ¡¡Dibujan la letra Q en la tipografía llamada negrita de pizarra!!
Aunque estas imágenes no son una demostración, sí aportan más indicios para creer que Pi es un número normal. Además lo hacen de forma muy visual (espero que fácil de entender) y muestran cómo se puede hacer investigación matemática sobre problemas difíciles usando ideas muy intuitivas.
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.
Nota 1: Esta entrada se pudo votar en Menéame. ¡Gracias!
Nota 2: Esta entrada ha llegado al Olimpo en Divoblogger. ¡Gracias!
Nota 3: Quiero agradecer a Fran su amabilidad, dando todas las facilidades para escribir esta entrada. ¡Muchas gracias!
Nota 4: Esta entrada participa en la Edición 5.4: Martin Gardner del Carnaval de Matemáticas cuyo anfitrión es Gaussianos.
Para saber más:
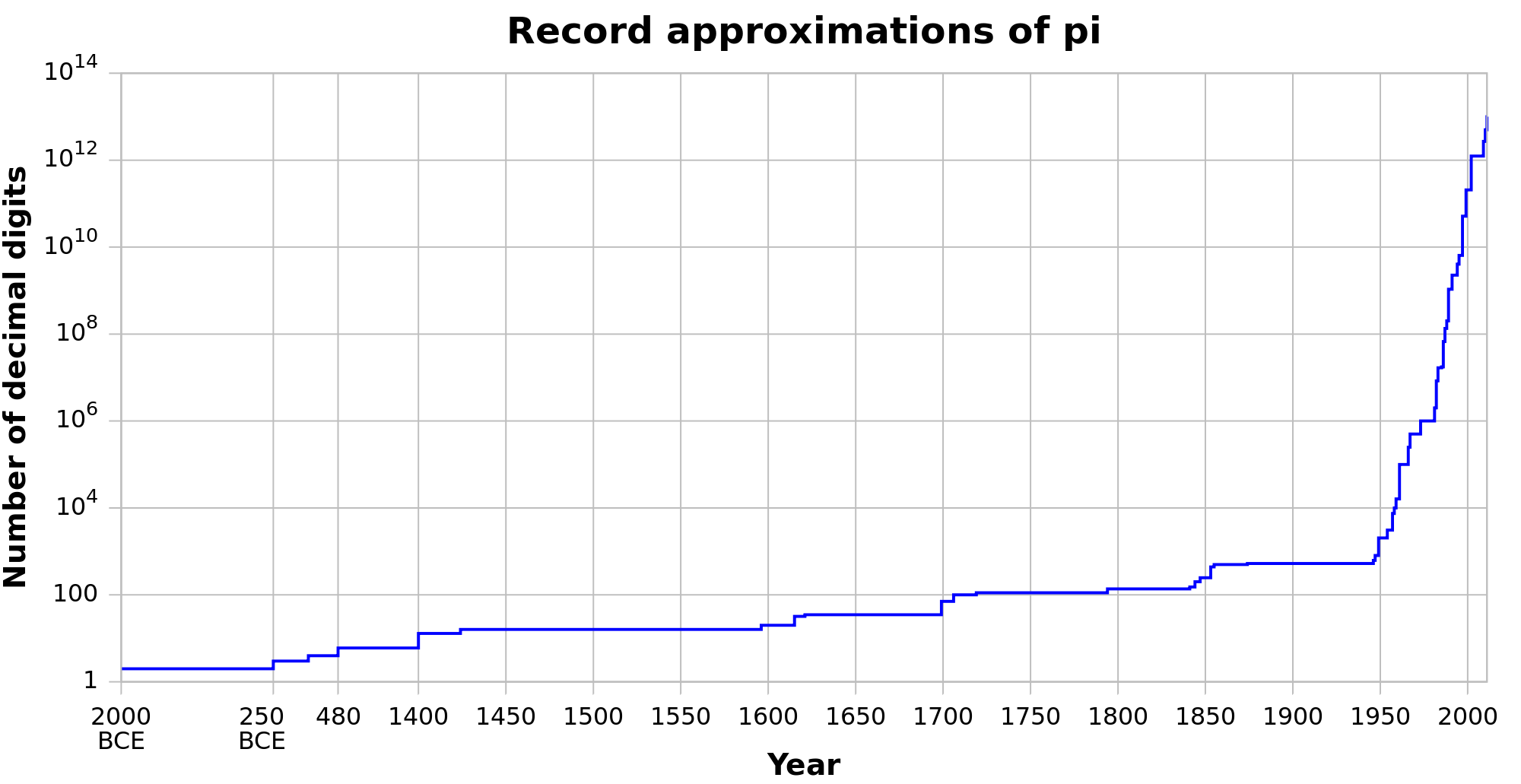
Si quieres comprobar cuánto han ayudado los ordenadores a conocer cada vez más dígitos del número Pi, puedes hacerlo en la siguiente gráfica que es… muy gráfica. Muestra un crecimiento notable a partir del año 1950, más o menos coincidiendo con la aparición del primer ordenador del mundo.
Al respecto, puede interesarte leer El algoritmo de Chudnovsky, o cómo se calculan los decimales de Pi en el siglo XXI, en Gaussianos.
En realidad, con la «técnica de la yenka» tal y como la has visto estás estudiando si Pi es normal en base 4 (para ver cómo puede servir también para otras bases puedes consultar la sección 3 del artículo Walking on Real Numbers). Pero es que no se sabe si Pi es normal o no para ninguna base. Hay otros números para los que tampoco se sabe, como (sqrt{2}), (log(2)) o el número e. En su artículo, Francisco Javier y sus coautores también obtienen la imagen de los primeros (10^6) dígitos del número e en base 4 que, como la de Pi, parece no tener ningún patrón (el origen de coordenadas marca el punto de inicio)
Si quieres saber más sobre cómo usar estas imágenes para medir de manera más precisa el parecido de Pi o e con un número normal, puedes leer la entrada We can learn a lot from a walk with real numbers que publiqué en Mapping Ignorance. Si quieres todavía más detalles, no dejes de leer el artículo Walking on Real Numbers de Francisco Javier y sus coautores.
Si tienes curiosidad por el tema pero no quieres enfangarte con demasiados detalles técnicos, te recomiendo la página del proyecto Walking on Real Numbers, donde puedes encontrar un montón de imágenes, artículos, transparencias y recortes de prensa (la imagen de Pi ha tenido bastante repercusión en los medios anglosajones, apareciendo en Wired y Gizmodo).
En cualquier caso, nadie te puede explicar esta investigación mejor que el propio Francisco Javier. Gracias a CIDlabs puedes ver y/o escuchar su charla Caminando sobre los números reales, sobre la que tienes más información en el blog de Tito Eliatron.
En general, la técnica de los caminos aleatorios resulta útil en muchos campos. Al respecto, puedes leer también esta traducción del libro Mathematical Circus del que probablemente haya sido el mejor divulgador matemático, Martin Gardner (al que está dedicada la presente edición del Carnaval de Matemáticas).
Y para terminar, como el baile de la yenka fue canción del verano en 1965, no puedo dejar de recomendarte que escuches la que puede ser la canción matemática de este verano, «Fermat, te has pasado macho», que forma parte del monólogo con el que mi compadre Aitor Menta ha quedado tercero en la presente edición del concurso Famelab de monólogos científicos (siguiendo la tradición de premios iniciada por Eduardo Sáenz de Cabezón). ¡Enhorabuena!
(Si tienes mucha prisa, puedes ir a la canción directamente).
Imágenes:
La imagen del dado de diez caras es de wiredlizard, en Wikimedia Commons. La imagen del joystick es de Kristine, en Flickr. La gráfica del número de dígitos de Pi conocidos (en base 10) es de Nageh, en Wikimedia Commons. El resto de imágenes están tomadas, con permiso de Francisco Javier Aragón Artacho, del artículo Walking on Real Numbers. El vídeo está incrustado con el permiso de su propietario, la Fundación Española para la Ciencia y la Tecnología.









Deja una respuesta