Es posible que conozcáis la paradoja del cumpleaños, pero para aquellos que no, ¿cuál creéis que sería la probabilidad de que en un grupo de 27 personas (una fiesta, reunión, en un bar…) haya al menos dos que cumplan el mismo día?
Por lo general, la gente dice “uf, tiene que ser mucha casualidad, será una probabilidad muy pequeña”.
Pues lo cierto es todo lo contrario, de hecho, para 23 o mas, ya supera el 50%, en el caso de 27 personas como hemos propuesto, nos encontramos con un 62,7% de probabilidad de que haya dos personas que cumplan los años el mismo día.
Haciendo la reflexión matemática, debemos tomar un número de personas ![]() puesto que para grupos mayores de 365 la probabilidad es 1 (100%).
puesto que para grupos mayores de 365 la probabilidad es 1 (100%).
Calculamos una probabilidad “p” de que no haya dos personas que cumplan los años el mismo día y después realizamos 1-p para hallar la probabilidad de que haya al menos dos personas.
Ahora bien, la probabilidad de que una persona no coincida con otra en su cumpleaños es casos favorables (todos los días del año excepto uno) entre casos posibles, de esta manera ![]() . Si incluimos otra persona, la probabilidad de que no coincida será de
. Si incluimos otra persona, la probabilidad de que no coincida será de ![]() y así sucesivamente.
y así sucesivamente.
Por tanto, y según la regla del producto, la probabilidad para dos o mas sucesos independientes (Es independiente por que si coincide un cumpleaños, no implica que pueda coincidir otro, no influye), es igual al producto de sus probabilidades individuales. Es decir, para n personas tendremos la expresión:
![]()
Expresada con factoriales
![]()
Esta es la probabilidad de que no coincida el cumpleaños de dos personas. Si queremos la probabilidad de que haya al menos dos personas que cumplan el mismo día, la expresión será 1-p.
Es decir :
![]()
Si tomamos algunos valores.
Para n=15 obtenemos una probabilidad de 0.253.
Para n=23 ya pasamos el 50%, exactamente obtenemos una probabilidad de 0.507.
Para n=27, obtenemos 0.627.
Para n=40, llegamos casi al 90%, con 0.891.
Para n=80, el resultado es de 0.99991, más del 99%.
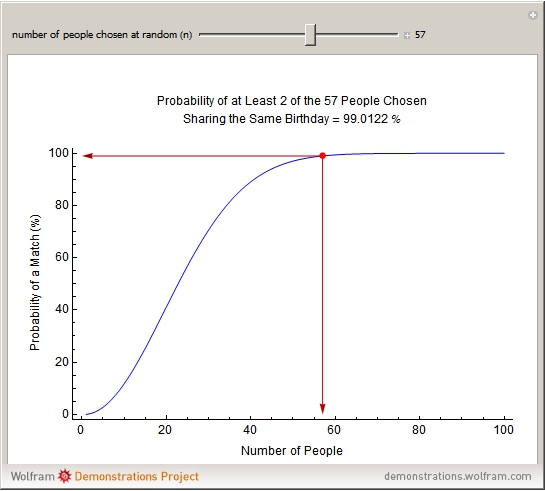
Podemos juguetear un poco con este simulador, para distintos valores de n.
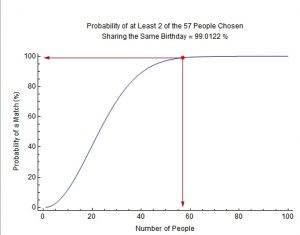
La gráfica que nos encontramos es la siguiente:
Normalmente cuando nos planteamos el problema solemos pensar en encontrar alguien que coincida con nuestro cumpleaños, cuando en realidad buscamos a cualquier pareja de dos personas del grupo que cumplan el mismo día. Evidentemente si buscamos a alguien que coincida con nosotros la probabilidad será muy pero que muy baja.
En conclusión, fíate de la razón pues la intuición no te dará la solución.
Imagen: Wolfram Demonstration
Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.


Responder a Cornelius Cancelar la respuesta