Esta es la historia de cómo un acertijo que parece inocente, sacado del escaparate de una tienda de niños, puede hacernos aprender más de lo esperábamos: En un cuarto hay varios gatos, cada gato en un rincón, cada gato ve tres gatos. ¿Sabes cuántos gatos son?

Si te encuentras este acertijo en un libro de adivinanzas infantiles, lo más probable es que respondas que hay cuatro gatos, pases página y no le des más vueltas. Por ejemplo, un gato en cada esquina de un cuadrado.

Pero, ¿estás seguro de que ésa es la única posibilidad? Chin, chin, chin, chiiin.

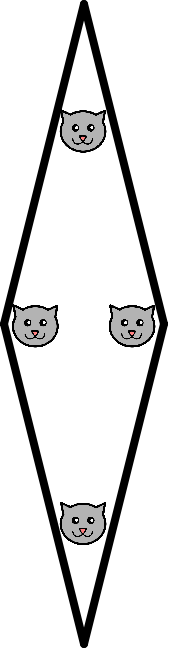
Te propongo que cambies un poco el cuarto de la figura anterior, para que tenga forma de rombo. Seguirás teniendo cuatro esquinas con un gato en cada una. En total cuatro gatos, como antes.

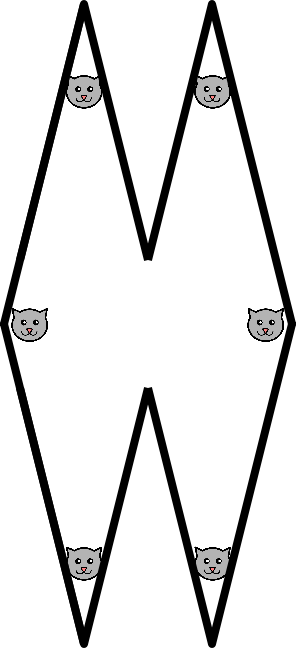
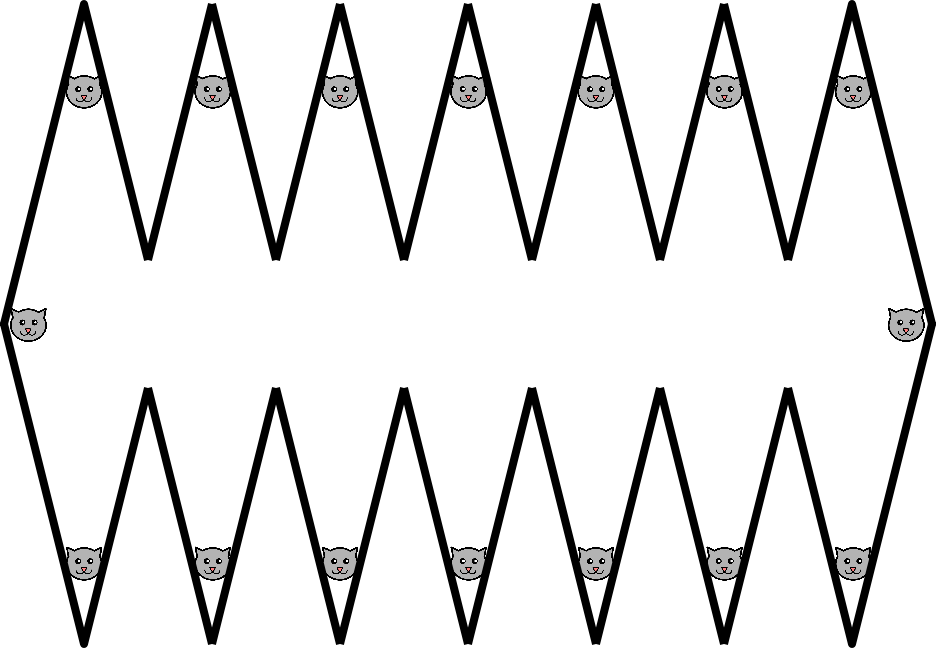
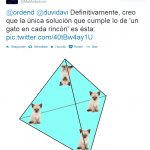
Ahora pon otro rombo al lado del anterior, en horizontal, tocándose en un punto. Tendrás dos rombos, igualitos que los de la televisión hace un tiempo. Prueba a abrir un pasillo entre los dos rombos, ensanchando ese punto en que se tocaban. Y coloca un gato en cada rincón… Tendrás seis gatos.

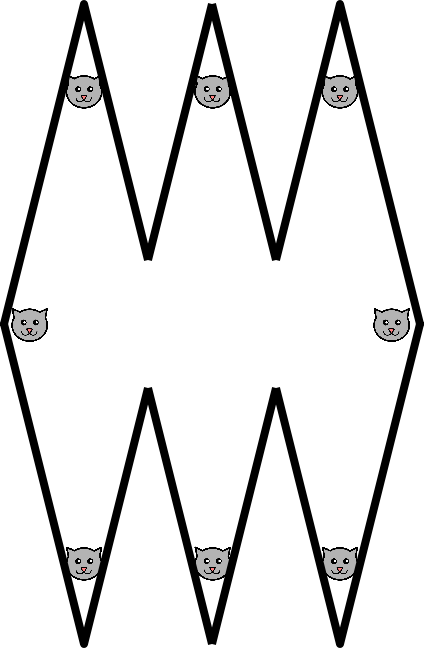
Así que añadiendo un rombo consigues dos gatos más. ¿Por qué no pruebas a añadir otro rombo? Tendrás tres rombos y, tachán, tachán, dos gatos más. O sea, ocho gatos.

Y puedes seguir haciendo esto hasta que te aburras, por ejemplo hasta tener siete rombos y dieciséis gatos.

Total, que tienes:

• Para 1 rombo, 4 gatos.
• Para 2 rombos, 6 gatos.
• Para 3 rombos, 8 gatos.
• …
• Para 7 rombos, 16 gatos.

En el primer rombo tenías 4 gatos y cada vez que añades un rombo estás añadiendo dos gatos, así que el número de gatos es «dos veces el número de rombos más dos». Es decir: [text{Numero de gatos}=2cdot(text{Numero de rombos})+2]

Esto es un número par (porque ambos sumandos son múltiplos de 2) y vale por lo menos cuatro (porque el número de rombos es por lo menos 1). Así que puedes conseguir cualquier número par de gatos a partir de cuatro.

¿Y ya está?

Si con esto te quedas tranquilo y no sigues leyendo, no seré yo quien lo critique… pero ¿no te pica un poco la curiosidad? ¿Y si hubiera otras posibilidades? Por ejemplo, ¿podrías conseguir un número impar de gatos haciendo otro tipo de dibujo?

Ahora es cuando tomas papel y lápiz y te pones a hacer dibujos como un loco. Después de un rato, estarás convencido de que no puede ser. Pero ¿por qué? La explicación es muy sencilla y tiene que ver con el Lema del Apretón de Manos:

•  Cada gato ve a otros tres, así que el número de “visiones” será tres veces el número de gatos [text{Numero de visiones}=3cdot(text{Numero de gatos})]
• El número de visiones tiene que ser un número par, porque si un gato ve a otro, éste también le ve a él (la visibilidad es recíproca). Así que (text{Numero de visiones}=3cdot(text{Numero de gatos})) es un número par.

¡¡Pero eso solo puede pasar si (text{Numero de gatos}) es par!! Así que ahora ya puedes asegurar que la respuesta matemática al acertijo sería

El número de gatos puede ser cualquier número par a partir del cuatro.

Por supuesto, esto no tiene en cuenta que la visión de los gatos es limitada, ni que nadie tiene en su casa un cuarto tan raro ni tan grande… Pero ya sabes que para un matemático las vacas son esféricas 🙂

Recuerda que puedes seguirnos en Twitter, en Facebook y en Google +.

Nota 1: Esta entrada ha llegado a portada en Menéame. ¡Gracias!

Nota 2: Esta entrada ha llegado al Olimpo en Divoblogger. ¡Gracias!

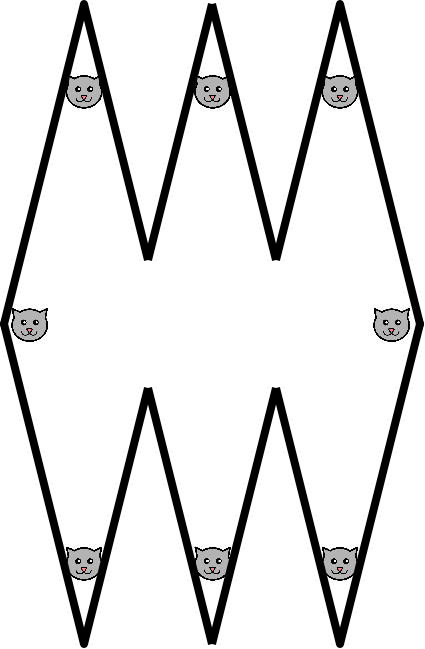
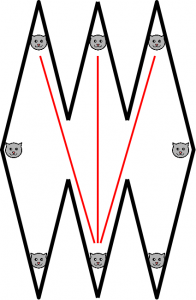
Nota 3: A algunos lectores les parece que, con más de dos rombos, no es cierto que cada gato vea tres gatos. Espero que esta imagen lo aclare.

Para saber más:

Quizá estés pensando qué pasa si el cuarto tiene que ser convexo (puedes mirar la entrada sobre el problema sin resolver en tu piscina). ¿Te atreves a dar una solución en ese caso?
Los problemas de visibilidad son una rama importante de la Geometría Computacional. Si quieres saber más sobre este tipo de problemas, te recomiendo el artículo divulgativo Iluminación y vigilancia en las Galerías de Arte, de mi colega Gregorio Hernández Peñalver. También es muy recomendable la entrada Teorema de la galería de arte de Raúl Ibáñez. Ya en inglés, puedes consultar el libro Art Gallery and Illumination Problems, de Jorge Urrutia.

Y si te gusta y quieres pasar a la historia resolviendo algún problema abierto en este campo, puedes consultar esta lista que, aunque no está muy actualizada, te dará una idea del tipo de cosas que uno se puede preguntar.

Imagen: 

El icono del gato es de pitr, en openclipart.

Vuestras aportaciones: 

Para terminar, es de justicia incluir aquí las aportaciones que me habéis hecho llegar sobre el acertijo. En realidad la primera de ellas fue anterior a la entrada con el acertijo; fue mi ex-alumno Alberto Cuesta quien me apuntó que la solución obvia de cuatro gatos no era la única. Además de las imágenes de la galería, hay más aportaciones en los comentarios a la entrada anterior. ¡Gracias a todos!