No te mates, que no hay manera le decían los otros dos alumnos a su compañero. Habían venido a resolver unas dudas y, cuando ya se iban, uno preguntó cuándo aparecería otro reto en el blog. Es que tengo un amigo al que siempre se los cuento, dijo. No me pude resistir. Y ahí seguía, un buen rato después, intentando evitar triángulos tricolores.

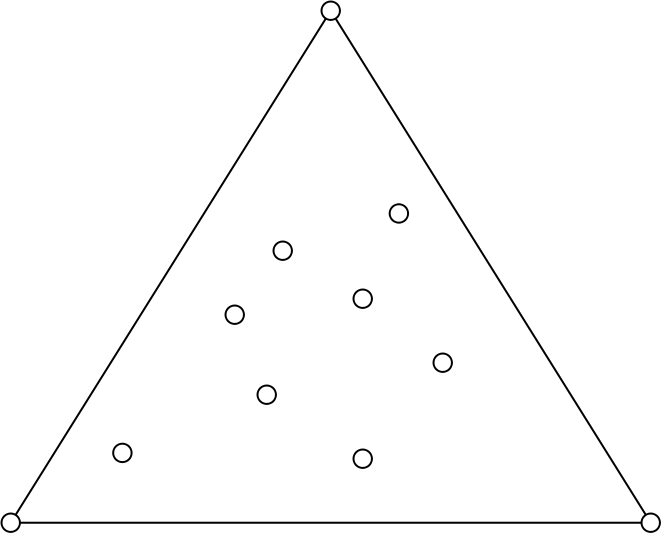
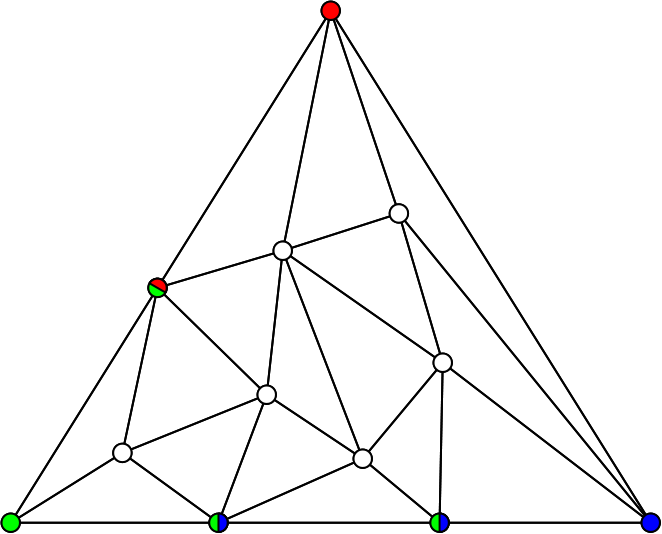
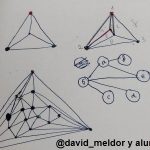
Dibuja un triángulo con unos cuantos puntos dentro. ¿Como quiera? Como te dé la gana.

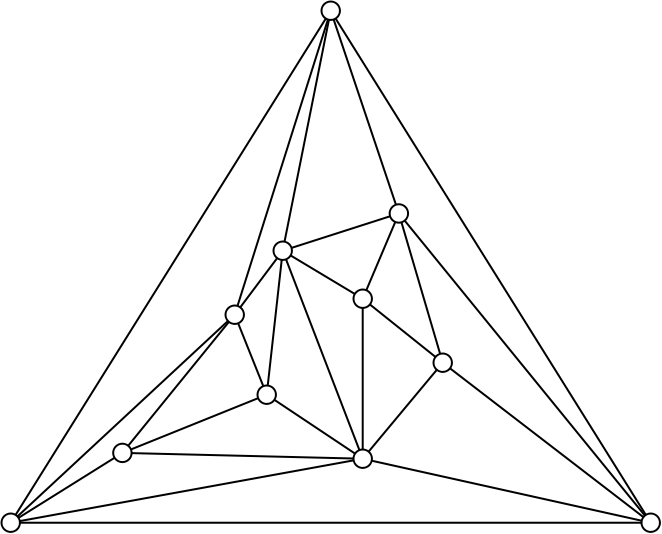
Luego une los puntos, dibujando todos los segmentos que puedas sin que éstos se crucen. ¿Pero como quiera? Como más rabia te dé. Cuando termines, comprueba que dentro solo tienes triángulos más pequeños.

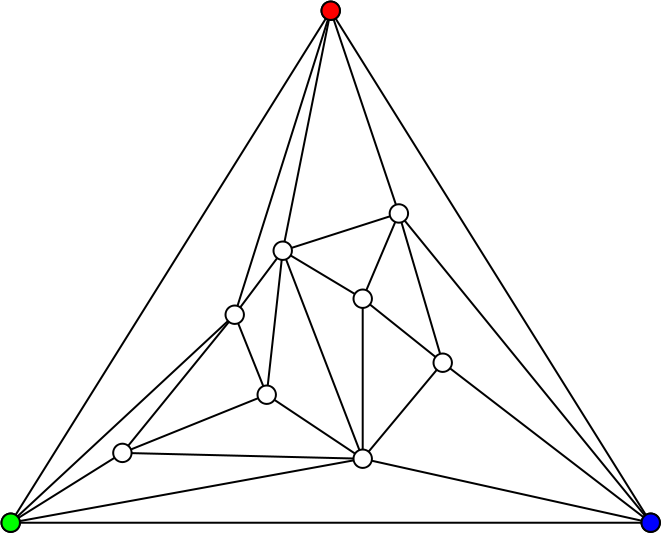
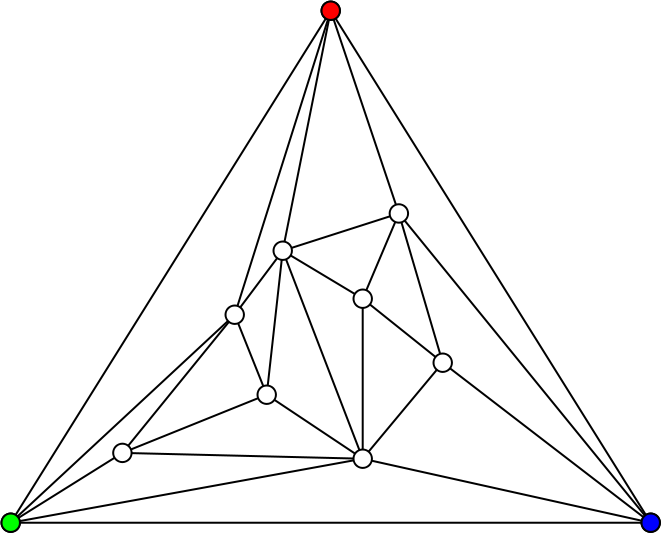
Ahora pinta los vértices del triángulo exterior con tres colores distintos; por ejemplo rojo, verde y azul. ¿También como yo quiera? También.

Aquí va el reto:

¿A que no consigues colorear el resto de puntos de manera que ninguno de los triángulos pequeños sea tricolor (con vértices rojo-verde-azul)?

Al final tuvimos que irnos, pero sé que se picó y esa tarde volvió a pasar un buen rato intentándolo…

Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.

Nota 1: Esta entrada ha resultado ganadora de la Edición 5.8: Betty Scott del Carnaval de Matemáticas, cuyo anfitrión es el blog tocamates (experto en proponer retos). ¡¡Gracias!!

Nota 2: Esta entrada (y su premio) va para Guillermo, Pablo y Adrián, por engancharse al blog y a la asignatura, haciendo que el esfuerzo se vea recompensado.

Nota 3: Si envías tu dibujo a cifrasyteclas@km77.com o @cifrasyteclas lo pondremos en la galería al final de la entrada.

Nota 4: Esta entrada está en Menéame.

Nota 5: Esta entrada ha llegado a portada en Divúlgame.

Nota 6: Esta entrada ha llegado a portada en Divoblogger.

Para saber más:

Lo hagas como lo hagas, no vas a poder evitar un triángulo tricolor, por el Lema de Sperner. Éste garantiza que el número de triángulos tricolores va a ser impar. Y como el cero es un número par, tendrá que haber algún triángulo tricolor.

Este lema es el análogo combinatorio del Teorema del punto fijo de Brouwer que se puede explicar, de manera simplificada, con un ejemplo muy gráfico: Prepara una taza de café y saca una foto de su superficie. Después remueve el café, como te dé la gana, y vuelve a sacar una foto de su superficie. Habrá un punto que ocupará exactamente la misma posición antes y después de remover (el punto fijo). Te recomiendo comprobar otros ejemplos en la página Math Images.

Tanto el Lema de Sperner como el Teorema del punto fijo de Brouwer juegan un papel importante en la búsqueda del equilibrio de Nash (el de la película Una mente maravillosa), que es crucial en Teoría de juegos (y por tanto en Economía). Por ejemplo, el equilibrio de Nash para el juego de Piedra, papel o tijera se obtiene al elegir con igual probabilidad cualquiera de las tres opciones.

El Lema de Sperner se puede demostrar de forma bastante simple usando teoría de grafos (puedes leer la demostración en la Wikipedia). Puedes encontrar una demostración diferente en este pdf de Alex Wright en el que, además, muestra cómo se puede usar el Lema de Sperner para demostrar el Teorema del punto fijo de Brouwer.

En tus dibujos, quizá algún triángulo te haya quedado muy pequeño, incluso de área nula (si sus tres vértices están sobre una misma recta). Para evitar esto, se suele pedir que no haya tres puntos alineados (una de las condiciones de la posición general).

El Lema de Sperner también funciona si colocas puntos sobre los lados del triángulo exterior. Con la única condición adicional de que esos puntos hay que pintarlos del mismo color que alguno de los extremos de ese lado. Pero de esto ya hablaremos en una entrada que está por venir.

Imágenes:

La imagen de la taza de café es de Anil Wadghule, en Flickr. El resto de imágenes son de creación propia. Todas ellas tienen licencia Creative Commons.

Vuestras aportaciones: