Vais a compartir piso. Toca distribuir habitaciones y decidir cómo repartir el precio. Quizá penséis dividir el precio en partes iguales, pero ¿y si una habitación es bastante más grande que las otras? Podríais pagar según los metros cuadrados, pero ¿y si nadie quiere pagar más por la habitación más grande? Estas aplicaciones interactivas usan matemáticas para que encuentres, de forma cómoda, un reparto justo que deje contento a todo el mundo.
Aunque en la vida real las cosas pueden ser bastante más complicadas, para ilustrar el método nos servirá este ejemplo:
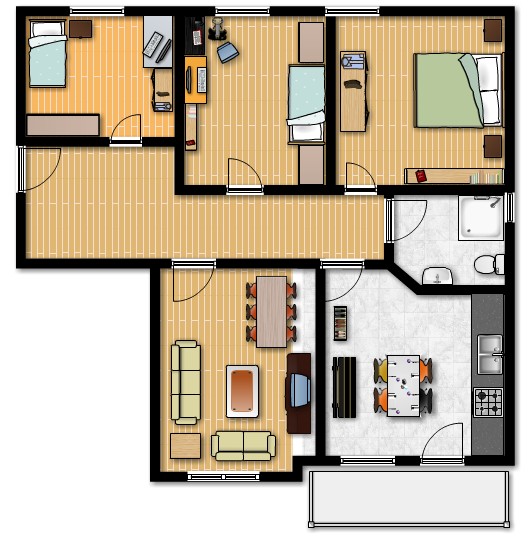
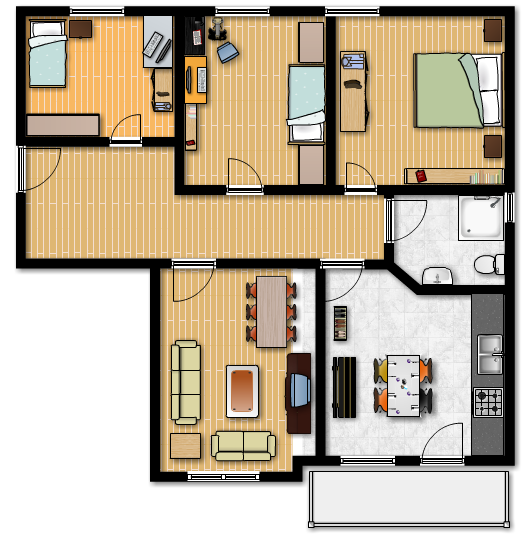
Alicia, Benito y Carlos quieren compartir un piso, de tres habitaciones, que cuesta 1000 euros al mes.
- Alicia prefiere la habitación de la derecha, la más grande, pero no puede pagar más de 300 euros al mes. De las otras dos habitaciones prefiere la de la izquierda.
- Benito también prefiere la habitación de la derecha pero, aunque es quien más dinero tiene, prefiere elegir otra habitación antes que pagar más que sus compañeros.
- Carlos solo quiere la habitación del medio. En la de la derecha le molestan los ruidos del baño y en la de la izquierda los de la escalera. Es el que menos dinero tiene de los tres.
¿Cómo repartir las habitaciones, y distribuir los 1000 euros de alquiler, para que todos queden contentos?
Para gente con prisa
Si estás en un situación de este tipo y tienes prisa por repartir el alquiler, puedes ir directamente a la aplicación interactiva de The New York Times.
También puedes usar la aplicación Spliddit, que además sirve para repartir una herencia o los méritos de un trabajo en grupo.
Para entender cómo se puede conseguir un reparto justo
La aplicación del The New York Times se basa en el reto tricolor que te propuse hace algunas entradas. La idea es pintar con tres capas una figura llena de triángulos y luego encontrar un triángulo «bien pintado».
Para empezar, los inquilinos eligen un sobrecoste aceptado (dentro chiste); una cantidad que a ninguno le importaría pagar de más sobre el precio que hubiera aceptado.
Este sobrecoste aceptado puede ser todo lo pequeño que se quiera, incluso un céntimo. Para que el ejemplo sea más sencillo de seguir, y no demasiado largo, vamos a imaginar un sobrecoste aceptado de 200 euros.
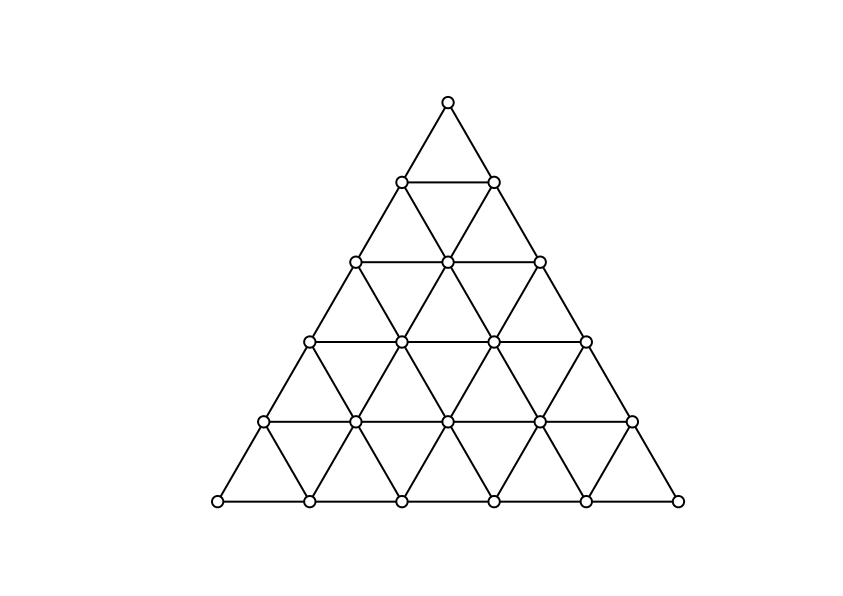
Como hay tres compañeros de piso, dibujamos un triángulo. Después dividimos el alquiler entre el sobrecoste aceptado ![]() y construimos una malla triangular partiendo cada lado del triángulo en ese número de trozos (en nuestro caso cinco):
y construimos una malla triangular partiendo cada lado del triángulo en ese número de trozos (en nuestro caso cinco):
Capa 1: Inquilino
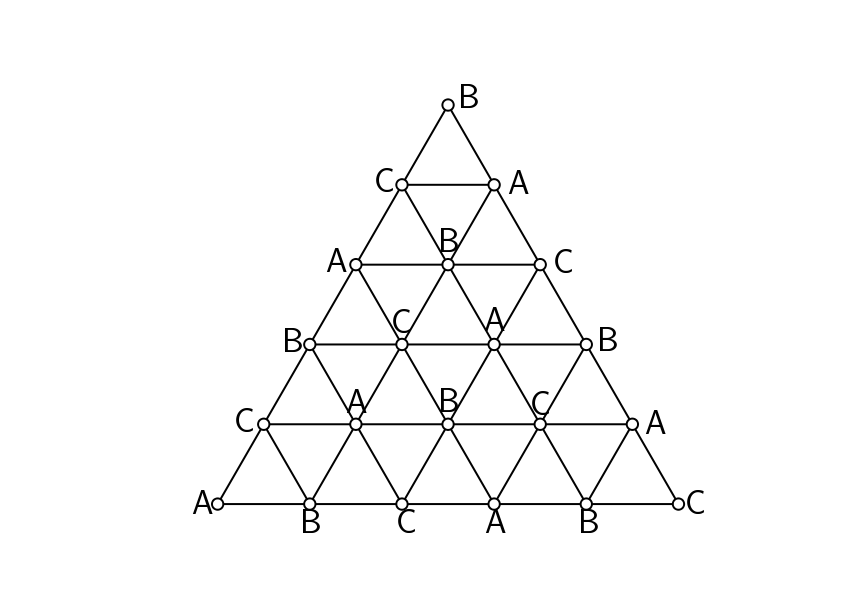
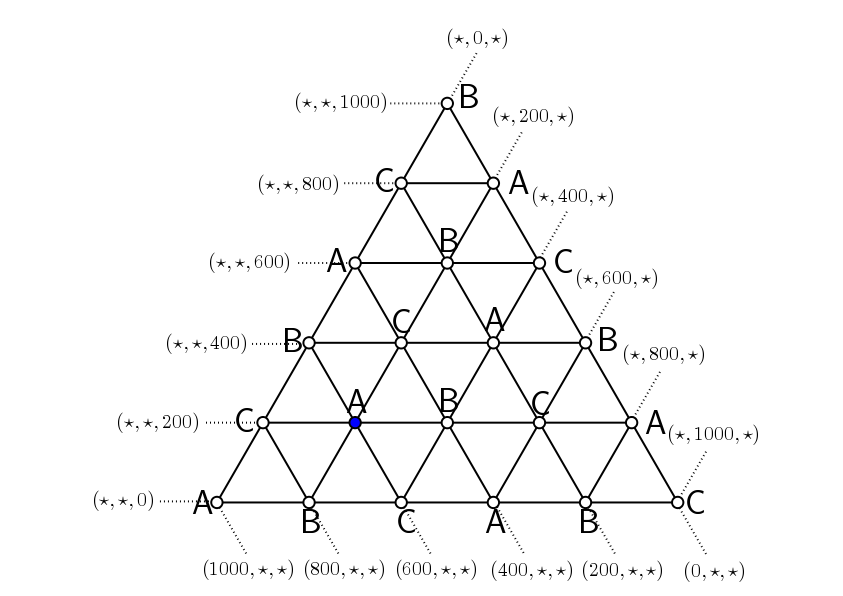
En la primera capa «pintaremos» cada punto de la malla con la inicial de uno de los inquilinos, A, B, C:
- Los vértices de los lados los pintamos siguiendo el patrón A – B – C – A – B – C – … – A – B – C.
- Para el resto de vértices, seguimos ese mismo patrón en cada horizontal.
Podemos comprobar que, de esa manera, todos los triángulos pequeños tienen vértices ABC.
Capa 2: Precios
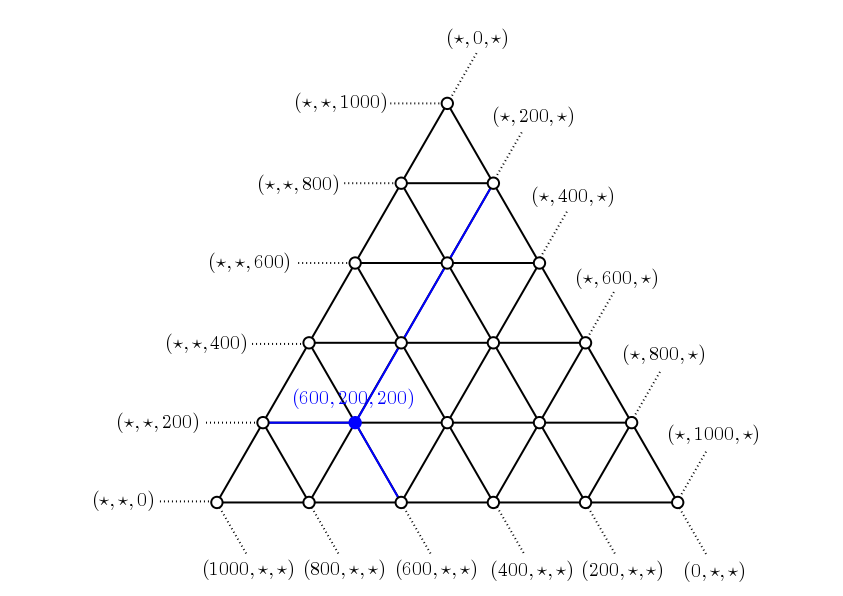
En la segunda capa, «pintaremos» cada punto de la malla con una combinación de precios. Lo haremos usando coordenadas baricéntricas, tres números que te dicen cuántas paralelas a cada lado te has tenido que mover para llegar al punto:
Cada coordenada representa el precio de una habitación. Por ejemplo, el punto (600,200,200) representa la combinación de precios «600 euros la habitación de la izquierda», «200 euros la del medio» y «200 euros la de la derecha».
Capa 3: Habitación preferida
A estas alturas cada punto de la malla está «pintado» con la inicial de un inquilino (Capa 1) y una combinación de precios (Capa 2). En la tercera capa pintaremos qué habitación preferiría ese inquilino si las habitaciones tuvieran esos precios.
Si prefiere la habitación izquierda, pintaremos el punto de rojo. Si prefiere la habitación del medio, lo pintaremos de verde. Si prefiere la habitación de la derecha, lo pintaremos de azul.
Como en nuestro ejemplo el punto (600,200,200) estaba pintado con la A de Alicia, le preguntamos a ésta qué habitación preferiría si costaran «600 euros la de la izquierda», «200 euros la del medio» y «200 euros la de la derecha».
Alicia responde que preferiría la habitación de la derecha, así que ese punto lo pintamos de azul. Y seguimos preguntando hasta pintar todos los puntos.
(Como en los lados exteriores una habitación sale gratis, ésa es la que eligen todos. Por eso en cada lado todos los puntos tienen el mismo color).
Juntamos las tres capas y ¡¡¡¡tacháááááán!!!!
Las matemáticas garantizan que
En esa figura siempre habrá algún triángulo con un vértice rojo, otro verde y otro azul.
En nuestra imagen anterior eso pasa en el triángulo resaltado:
- La A está en rojo, así que Alicia se quedará con la habitación de la izquierda.
- La B está en azul, así que Benito se quedará con la habitación de la derecha.
- La C está en verde, así que Carlos se quedará con la habitación del medio.
¡¡Ya sabemos cómo repartir las habitaciones!! Falta ver que ese reparto deje a todos contentos:
- Alicia eligió esa habitación (izquierda) con un precio de 200 euros (primera coordenada).
- Benito eligió esa habitación (derecha) con un precio de 200 euros (tercera coordenada).
- Carlos eligió esa habitación (medio) con un precio de 200 euros (segunda coordenada).
Seguro que ya te has dado cuenta de que esos precios suman 600 y no llegan a los 1000 euros del alquiler. Por eso ahora entra en juego el sobrecoste aceptado: Si esos 400 euros que faltan los reparten por igual entre los tres, cada uno tendrá un sobrecoste de 400/3=133.33…, más pequeño que el aceptado.
Con ese reparto de habitaciones y pagando cada uno 333.33 euros, todos contentos (el céntimo que falta se lo pueden ir turnando 😉 ).
Recuerda que puedes seguirnos en Twitter, en Facebook, en YouTube y en Google +.
Nota 1: Esta entrada ha llegado a portada en Menéame. ¡Gracias!
Nota 2: Esta entrada participa en la Edición 6.2 del Carnaval de Matemáticas, cuyo blog anfitrión es La Aventura de la Ciencia.
Dedicatoria:
Quiero dedicar esta entrada a mi querido y admirado director de tesis Paco Santos. Entre lo mucho que le debo está haberme descubierto el Lema de Sperner (el del reto tricolor) y haberme llevado con él de estancia a la UC Davis. Allí un día aparecieron unas estudiantes en el despacho que compartíamos, preguntando cómo repartir de forma justa su alquiler. Estábamos enfrascados trabajando, así que en vez de contarles este método las convencimos para que fueran a preguntar al departamento de Derecho.
Para saber más
El resultado que garantiza un triángulo tricolor es una versión «vitaminada» del Lema de Sperner que te conté en la entrada del reto tricolor.
Lo demostró Francis Su (actual presidente de la Mathematical Association of America) en su artículo Rental Harmony: Sperner’s Lemma in Fair Division (pdf) de 1999. Para que funcione hacen falta unas condiciones bastante razonables:
- Para cualquier combinación de precios, todos los inquilinos encuentran aceptable alguna habitación.
- Todos los inquilinos prefieren una habitación gratis antes que pagar por cualquier otra.
- Si un inquilino prefiere siempre la misma habitación para una secuencia de precios, también preferirá esa habitación para el precio al que tiende esa secuencia.
Este método de Su para repartir el alquiler ha aparecido, entre otros sitios, en The New York Times y en Science News. Además de la aplicación en The New York Times, quizá te interese ver la implementación del método que hizo el propio Su, disponible en su página web.
Si en lugar de repartir entre 3 hubiera que repartir entre 4, el método sería similar pero usando un tetraedro (3D) en lugar de un triángulo (2D). En general, para repartir entre (n) el método usa un (n-1) símplice (dimensión (n-1)).
La aplicación Spliddit usa un algoritmo diferente para repartir el alquiler, basado en el artículo Room assignment-rent division: A market approach. Para repartir herencias se basa en el artículo Impartial division of a dollar, que también usa para repartir de forma justa el orden de firmantes en un artículo científico.
Para saber aún más
Si divides cada lado del triángulo en (n) partes (en nuestro ejemplo era (n=5)), el número de triángulos pequeños en la malla será (n^2). Puedes demostrarlo sumando primero los triángulos que apuntan hacia arriba y luego los que apuntan hacia abajo:
- Apuntando hacia arriba hay (n) triángulos en la fila horizontal inferior, (n-1) en la fila horizontal por encima de ésta, (n-2) en la siguiente,… y así hasta (1) arriba del todo. En total el número de triángulos apuntando hacia arriba es [1+cdots +(n-1)+n = frac{(n+1)cdot n}{2}]
- Apuntando hacia abajo hay (n-1) triángulos en la fila horizontal inferior, (n-2) en la fila horizontal por encima de ésta, (n-2) en la siguiente,… y así hasta (1) triángulo que es el de más arriba entre los que apuntan hacia abajo. En total el número de triángulos apuntando hacia abajo es [1+cdots +(n-2)+(n-1) = frac{ncdot (n-1)}{2}]
La suma de estas dos cantidades es [frac{(n+1)cdot n}{2}+frac{ncdot (n-1)}{2} = frac{(n+1)cdot n + ncdot (n-1)}{2} = frac{ncdot ((n+1)+(n-1))}{2} = frac{ncdot 2n}{2} = n^2]
También puedes demostrar que en el Paso 1 es posible etiquetar la malla de modo que todos los triángulos pequeños tengan vértices ABC: Las etiquetas del triángulo exterior seguían el patrón A – B – C – A – B – C – … – A – B – C (bien en sentido horario o bien en sentido antihorario). Y para eso basta que el número de vértices en los lados del triángulo exterior sea múltiplo de tres. Pero eso pasa siempre, porque ese número de vértices es el triple del número de partes en que has dividido los lados del triángulo, es decir, (3n).
Imágenes
La imagen con el plano de un piso es de badcrc, en Flickr y el resto de imágenes son de creación propia. Todas tienen licencia Creative Commons.



Deja una respuesta